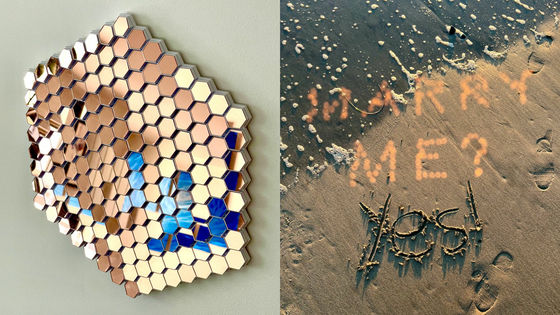超複雑な形状なのに鏡像なしで非周期に並べてタイル張り可能な新しい図形「Spectres(スペクター:怪物)」が見つかる
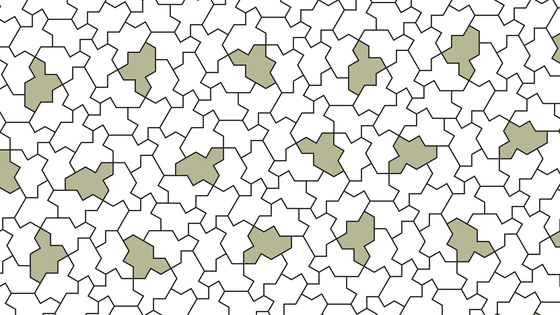
右手と左手のように、「ある構造」と「その鏡像の関係にある構造」が回転操作によって互いに重ね合わせることができない構造として存在することをキラリティー(対掌性)と呼びます。キラリティーでありながら非周期なモノタイルでもあるという新しい図形「Spectres(スペクター:怪物)」を研究チームが発見しました。
A chiral aperiodic monotile
https://cs.uwaterloo.ca/~csk/spectre/
Now that’s what I call an aperiodic monotile! | The Aperiodical
https://aperiodical.com/2023/05/now-thats-what-i-call-an-aperiodic-monotile/
タイル(図形)で平面(境界を除き)を隙間なく埋めることができることを、「平面のタイル張り(テセレーション)」と呼びます。すべてのタイルが同じサイズ・形状である場合のタイル張りを「モノヘドラル」、モノヘドラルで裏返したタイルを利用することを「モノタイル」を呼びます。
このタイル張りについて研究するグループが、2023年3月に非周期的なモノタイルを発見しました。この時発見されたのが以下の図形で、「hat(ハット:帽子)」と呼ばれるものです。
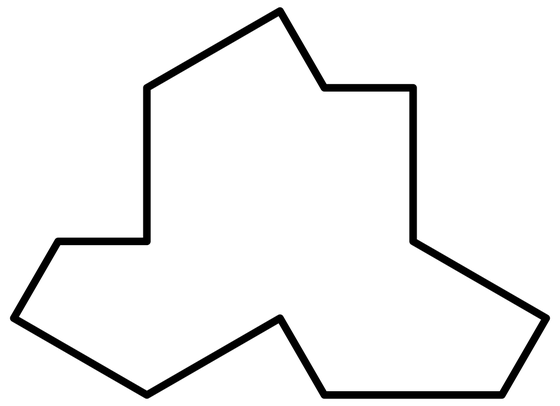
ただし、ハットの場合はタイル張りする際に6つに1つは鏡像を利用する必要がありました。

そのため、「移動と回転のみで非周期性を実現できるのか?」という問題が残っていたそうです。そんな中、同研究チームが問題を解決することができる形状、つまりは「鏡像を伴わずに平面を非周期的にタイル張りすることができる形状」を新しく発見しました。
新しく発見された形状は「Spectres(スペクター:怪物)」と呼ばれており、研究チームはこの形状を「キラリティーな非周期モノタイル」と表現しています。なお、「キラリティーな非周期モノタイル」では図形の反射が許可されているものの、「スペクターは移動と回転だけで非周期タイル張りが可能になる」そうです。
スペクターは辺を変形させてもタイル張りすることができるとのことで、研究チームは以下の3つのバリエーションを公開しています。
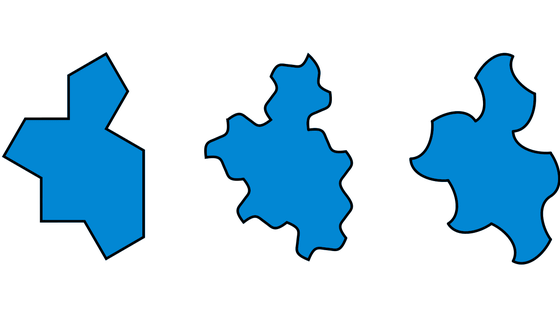
実際にスペクターを並べてタイル張りを行うと以下のようになります。
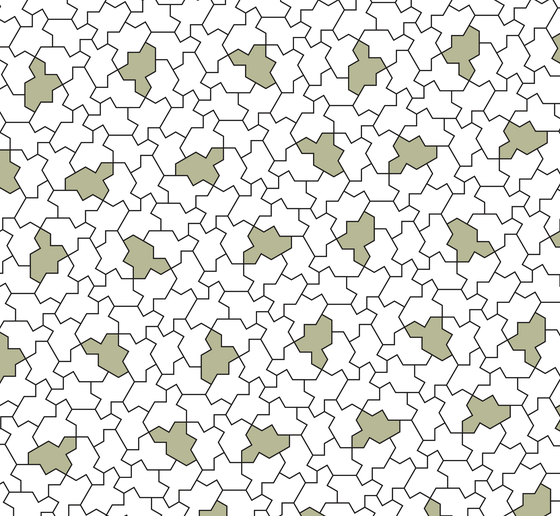
研究者のひとりであるクレイグ・S・カプラン氏は、「新しい図形を発見しました!私たちの古い論文にある『周期的にタイルを張ることができる形状』は、非周期的にタイルを張るように修正することができると判明しました。鏡像なしにです」と語りました。
New shape just dropped! It turns out that the one shape in our old paper that tiled periodically (known as Tile(1,1) there) can be modified to tile aperiodically *without reflections*. More info at https://t.co/pcCdPrwxUk, full thread at https://t.co/CNTekmPT3a
— Craig S. Kaplan (@cs_kaplan) May 30, 2023
なお、タイル張りの数理を専門とする荒木義明さんもスペクターについてツイートしており、「スペクターは辺を変形させることができる」という特徴を活かして線を変形させてみたり、スペクターをタイル張りする際の置換システムについて考察したりしているので、気になる人は同氏のTwitterアカウントもチェックしてみてください。
[BREAKING] A chiral aperiodic monotile finally discovered!
— Yoshiaki Araki 荒木義明 (@alytile) May 30, 2023
[速報] 鏡像なしの非周期モノタイルが発見される。
それも前回のTile(1,1)にマッチングルールをつけた形とな!辺を変形できるのでデザインしがいがありそう
何に見える?身近な何かに見立てみよう!#aperiodic https://t.co/nMpCPfecjN pic.twitter.com/75KG56meYi
また、タイル張りそのものに興味があるという人には以下のページもオススメです。
非周期的タイル張りのみ可能なタイルの話
https://tilingpackingcovering.web.fc2.com/memo_aperiodic_monotile.html
・関連記事
幾何学折り紙のパイオニアである藤本修三氏の自費出版折り紙教本5冊がパブリックドメインに - GIGAZINE
幾何学模様がどのような機械特性を持つか調査 - GIGAZINE
現実には不可能なレベルで複雑な折り紙を3Dモデルで簡単にシミュレートできるウェブアプリ「Origami Simulator」 - GIGAZINE
折り紙のパターンをロケットやエアバッグに応用する物理学者&折り紙アーティスト - GIGAZINE
「折り紙」構造を応用した小型・軽量ロボットが改良され、誤飲したボタン電池を体内から取り除ける「Ingestible Origami Robot」に進化 - GIGAZINE
数学好きが位相幾何学を応用してベーグルをカットするとこうなる - GIGAZINE
・関連コンテンツ
in サイエンス, デザイン, Posted by logu_ii
You can read the machine translated English article A new figure 'Spectres (Monster)' that c….