Jun 01, 2023 21:00:00

A new figure 'Spectres (Monster)' that can be arranged aperiodically and tiled without a mirror image even though it is a super complicated shape can be found

Chirality is the existence of structures that cannot be superimposed on each other by rotating operations, such as the right and left hands. A research team discovered a new figure ' Spectres ' that is both chirality and aperiodic monotile.

A chiral aperiodic monotile
https://cs.uwaterloo.ca/~csk/spectre/

Now that's what I call an aperiodic monotile!
https://aperiodical.com/2023/05/now-thats-what-i-call-an-aperiodic-monotile/

The ability to fill a plane (excluding boundaries) with tiles (shapes) without gaps is called 'plane tiling (tessellation)'. Tiling when all tiles are the same size and shape is called 'monohedral', and using tiles that are flipped over in monohedral is called 'monotile'.

A group researching this tiling discovered an aperiodic monotile in March 2023. At this time, the following figure was discovered, which is called ' hat' .

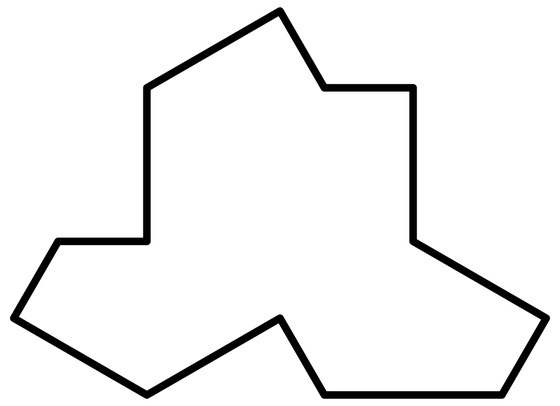
However, in the case of Hutt, one in six had to use a mirror image when tiling.

Therefore, it seems that there was still the problem of 'Is it possible to realize aperiodicity only by movement and rotation?' Meanwhile, the research team discovered a new shape that can solve the problem, that is, ``a shape that can aperiodically tile a plane without a mirror image''.

The newly discovered shape is called `` Spectres '', and the research team describes this shape as `` chirality aperiodic monotile ''. In addition, although reflection of figures is permitted in 'chirality aperiodic monotile', 'spector can be aperiodically tiled only by movement and rotation'.

Spector can be tiled even if the sides are deformed, and the research team has released the following three variations.

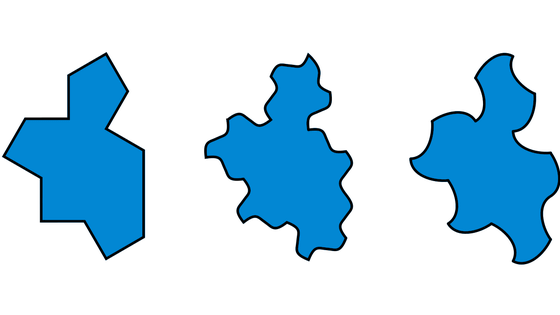
When the specters are actually arranged and tiled, it will be as follows.

One of the researchers Craig S. It turns out that it can be modified like this, without a mirror image.'

New shape just dropped! It turns out that the one shape in our old paper that tiled periodically (known as Tile(1,1) there) can be modified to tile aperiodically *without reflections*. More info at https://t. co/pcCdPrwxUk , full thread at https://t.co/CNTekmPT3a

—Craig S. Kaplan (@cs_kaplan) May 30, 2023

In addition, Mr. Yoshiaki Araki, who specializes in tiling mathematics, also tweeted about Specter, trying to transform lines by taking advantage of the feature that ``Spector can transform sides'' and tiling Specter If you are interested, please check his Twitter account as well, as he is considering the replacement system at the time.

[BREAKING] A chiral aperiodic monotile finally discovered!
[Breaking news] Aperiodic monotiles without mirror images are discovered.
It's also the form of adding a matching rule to the previous Tile(1,1)! The design seems interesting because the sides can be transformed. What does it look like? Let's look at something familiar! #aperiodic https://t.co/nMpCPfecjN pic.twitter.com/75KG56meYi

— Yoshiaki Araki Yoshiaki Araki (@alytile) May 30, 2023

Also, for those who are interested in tiling itself, the following pages are also recommended.

Talking about tiles where only aperiodic tiling is possible
https://tilingpackingcovering.web.fc2.com/memo_aperiodic_monotile.html