ヤフコメやYouTubeのコメント欄を非表示にできるブラウザ拡張機能「Shut Up」
ウェブページのコメント欄には役立つ情報が書き込まれている場合もありますが、不快なコメントやネタバレなどが書き込まれることもあります。ブラウザ拡張機能の「Shut Up」を使えば各種ウェブサイトのコメント欄を非表示にすることができます。
Shut Up: Comment Blocker
https://rickyromero.com/shutup/
Shut UpはChrome版、Firefox版、Edge版、Safari版、Opera版(Chromeウェブストア経由)が用意されています。今回はChrome版を使ってみます。
まずは以下のリンクをクリックしてChrome版Shut Upの配布ページにアクセス。
Shut Up: Comment Blocker - Chrome ウェブストア
https://chromewebstore.google.com/detail/shut-up-comment-blocker/oklfoejikkmejobodofaimigojomlfim
「Chromeに追加」をクリック。
「拡張機能を追加」をクリック。
画面右上に以下のポップアップが表示されたらインストールは完了です。
実際にShut Upの効果を確認してみます。まず、Shut UpをインストールしていないChromeでYahoo!ニュースにアクセスしてみます。
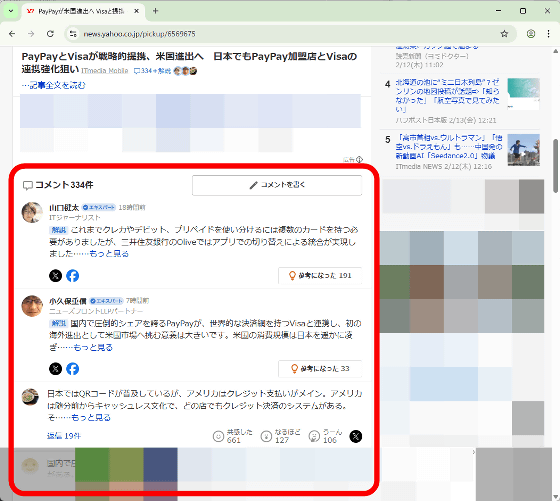
記事の下部にコメント欄が表示されました。
Shut Upインストール済みのChromeで同じページにアクセス。記事部分の見た目は変わっていません。
スクロールしてみるとコメント欄が消えていました。
少年ジャンプ+でも試してみます。通常のChromeだとページの下部にコメント欄が表示されています。
Shut Upをインストールするとコメント欄の枠は残っているもののコメントは消えました。これでうっかりネタバレを見てしまうリスクがなくなります。
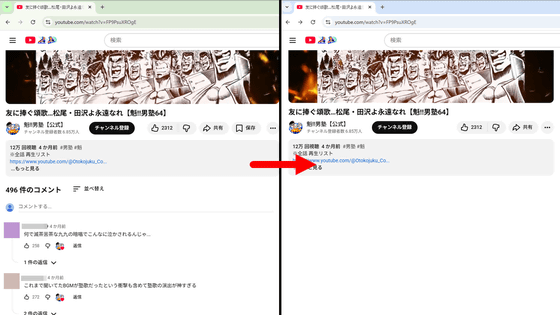
通常のChromeでYouTubeの動画を閲覧すると、動画の下部にコメント欄が表示されます。
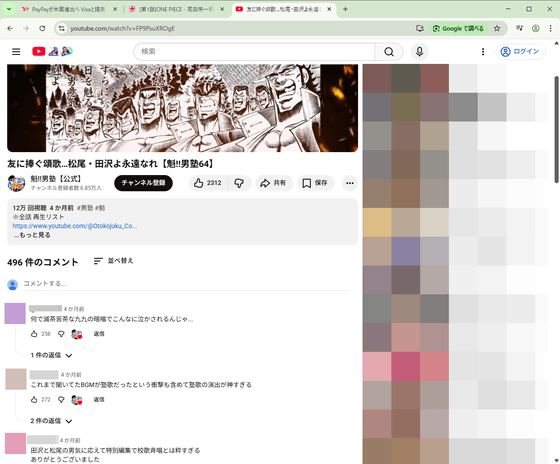
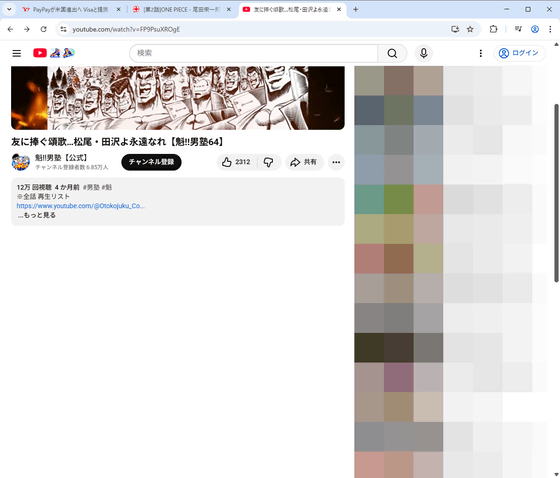
Shut Upをインストールすればコメント欄は表示されません。
コメントを見たいウェブサイトではコメントを表示することもできます。まず画面右上の拡張機能ボタンをクリックしてからShut Upのボタンをクリック。
これでコメント欄が復活しました。
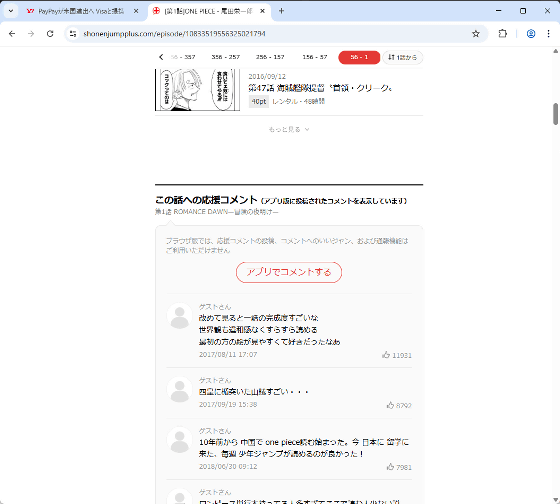
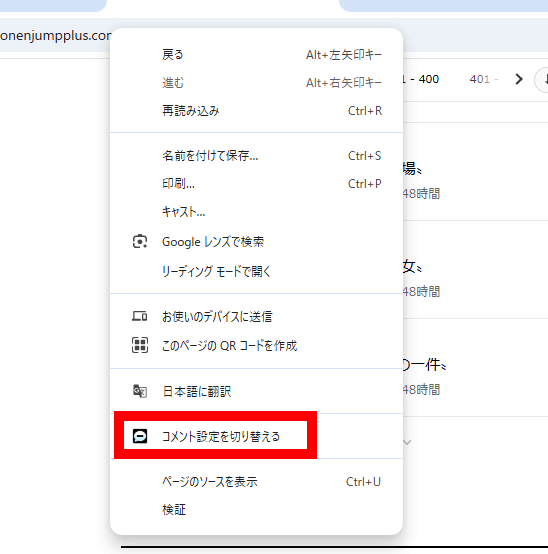
右クリックメニューからもコメントの表示・非表示を切り替えられます。
Shut Upの本体は「shutup.css」というCSSスタイルシートです。コードを見てみたところ、「.CommentBox,」とか「.Comment,」といった一般的なコメント欄で使われる要素を検知して非表示にしているほか、ウェブサイトによっては個別のコードで対応しているようでした。また、GitHubやSubstackなど一部のウェブサイトは例外サイトに指定されていました。
・関連記事
YouTubeの関連動画やコメントなどを非表示にできるブラウザ拡張機能「UnTrap for YouTube」レビュー、Android版FirefoxやiOS版Safariでも使えて広告スキップも可能 - GIGAZINE
ニコニコ動画で「ランキングの広告を非表示」「視聴ページの外観変更」などのカスタムを可能にする拡張機能「Niconico-PepperMint+」使用レビュー - GIGAZINE
ニコニコ動画の表示をすっきりさせてくれる「Niconico-PepperMint」をサクッと簡単にインストールして使ってみた - GIGAZINE
GitHubに100種類以上の機能を追加し、インターフェースを使いやすく改良するブラウザ拡張機能「Refined GitHub」 - GIGAZINE
記事からゴチャゴチャした表示を除外して読みやすくしてくれる「Unclutter」 - GIGAZINE
・関連コンテンツ
in ソフトウェア, レビュー, Posted by log1o_hf
You can read the machine translated English article 'Shut Up' is a browser extension that le….