「自分よりも自分の友だちの方が多くの友だちとつながっている」というのがネットワークの常識

「友だちの友だちはみな友だち」という言葉がある通り、私たちの生きる社会は各人の複雑な人間関係でつながったネットワークといえます。そんなネットワークにおいて「自分の友だちが持っている友だちの数は、自分の友だちの数よりも多い場合がほとんどである」という奇妙な法則について、理論物理学を研究するヴィネシュ・ケマニ氏が数学やシミュレーションを交えながらわかりやすく解説しています。

Your Friends Have More Friends Than You
https://scribe.citizen4.eu/your-friends-have-more-friends-than-you-e005796841bb

そもそも「友だちが自分よりも多くの友だちを持っている」とは、「自分の友だちが有する平均友人数」で示します。例えば、自分にN人の友だちがいるとします。そして、1人目の友だちにはF₁人の友人、2人目の友だちにはF₂人の友人というように、n番目の友だちが有する友人数はF_n人で表せるとします。この時、「自分の友だちが有する平均友人数＝＜F＞」は「(F₁＋F₂＋F₃＋……＋F_N)÷N」で表わされます。つまり、「友だちが自分よりも多くの友だちを持っている」というのは「＜F＞がNを上回る」と表現できます。

ケマニ氏によれば、現実の友人関係だけではなく、TwitterやLinkedInなどといったソーシャルネットワークでも＜F＞がNを上回るケースがよく見られるとのこと。ケマニ氏は「友だちが自分よりも多くの友だちを持っている」という状態が発生する理由について、グラフ構造を用いて説明しています。

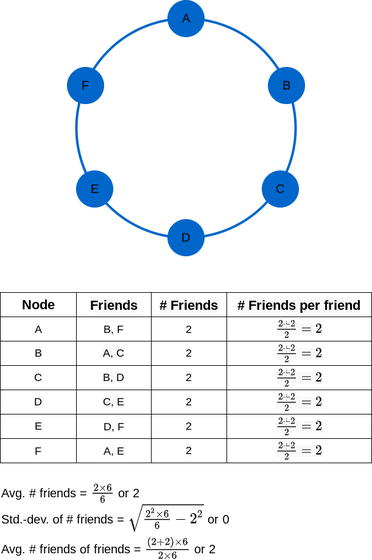
例えば、以下は6人で構成されるネットワークの実例。A～Fのアルファベットが書かれたノード部分が個人で、ノード同士を結ぶエッジが友情関係を示しています。6人それぞれに2人ずつ友だちがいる状態なのでネットワークは均等であるといえ、この時の状態は＜F＞＝Nと表わすことができます。

しかし、実際のネットワークは均等ではありません。上記のネットワークに、通常のノードよりもずっと多く接続されている外れ値のノード・Zを追加したところが以下。A～Fの友人数、すなわちNはそれぞれ3人で、Zだけは6人となっています。そして、A～Fにとって友だちが有している平均友人数、すなわち＜F＞は(3＋3＋6)÷3＝4人となり、A～Fの場合は＜F＞がNを上回ることになります。ただし、高度に接続しているノードであるZだけは、＜F＞がNを上回っていません。

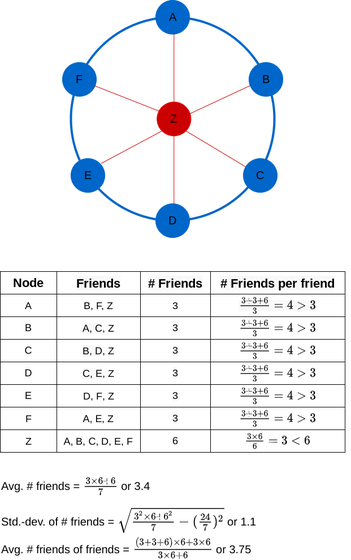
一般的に、あるネットワークに他のノードよりもはるかに高度に接続されているノードがf個ある場合、ネットワーク内の残りのノード1-f個のほとんどの接続数は、その接続先のノードよりも少なくなります。ほとんどの現実世界のネットワーク、特にソーシャルネットワークでは、高度に接続された外れ値のノードがごく一部存在しています。

1つのネットワークの中で、ノード当たりの平均接続数であるNをμ、ノード当たりの接続数の標準偏差をσとすると、接続ノードの平均接続数である＜F＞はμ＋σ²/μと表すことができます。μとσは正の実数なので、＜F＞は常にμ以上となります。そのため、自身の友人数よりも友人の平均友人数の方がだいたいの場合において上回るというわけです。

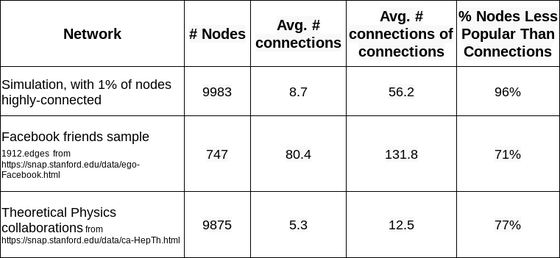
以下の表は3つのネットワークによる実例です。ネットワークは上から「高度に接続されたノードが1％含まれるネットワーク」「Facebookのネットワークの一部」「これまでの研究で使われたネットワークデータ」です。Nodesが「ノード数」、Avg. #connectionsが「ノード当たりの平均接続数」、Avg. #connections of connectionsが「接続ノードの平均接続数」、% Nodes Less Popular Than Connectionsが「平均接続数が接続ノードの平均接続数を下回ったノードの割合」です。この表を見ると、すべてのネットワークで「平均接続数が接続ノードの平均接続数を下回ったノード」、つまり「友だちが自分よりも多くの友だちを持っている人」がノードの大部分を占めていることがわかります。

この理屈を利用することで、「あるネットワーク内で接続されているノード間でローカルにやりとりされる情報の拡散に影響を与える」ことが可能になります。すなわち、ネットワーク内でどのノードが最も強く接続されているかがわかれば、それを利用して情報の拡散に影響を与えることができます。

例えば、うわさ話をネットワーク全体に広めたいと考えた時、ネットワークのメンバーをランダムに抽出してうわさ話を吹き込むよりも、ランダムに抽出したメンバーに友だちを選んでもらい、その友だちにうわさ話を吹き込む方が早く拡散されるとのこと。実際にシミュレーションした結果をまとめた以下のグラフを見ると、前者の方法(青色)よりも後者の方法(赤色)の方が拡散速度が早いとわかります。

また、あるコミュニティで感染症が蔓延していることを検知する場合、コミュニティのメンバーをランダムにピックアップして直接監視する(青色)より、ランダムにピックアップしたメンバーに友人を監視してもらう方(赤色)がより早く感染者を検知できるそうです。

さらに、新型コロナウイルスのように感染者が激増する中で、ワクチンが限られた数しかない場合、コミュニティからランダムに抽出したメンバーに予防接種を行う(青色)よりも、ランダムに抽出したメンバーのうちからさらにランダムで抽出した友人に予防接種を行った方(赤色)が、感染者数の増加を抑えることができるとのこと。

ケマニ氏は「あなたの友だちの方が、あなたよりも友だちが多い可能性が高いといえます。傷ついたり、ありえないと思ったり、あるいは単に風変わりだと感じるかもしれません。しかし、それは真実なのです」と述べています。