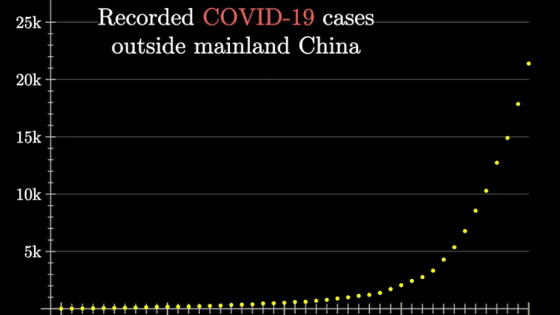
The common sense of the network is that ``my friends are connected to more friends than me''

As the saying goes, 'Friends of friends are friends,' the society we live in is a network of complex human relationships. In such a network, Mr. Vinesh Kemani, who studies theoretical physics about the strange law that ``the number of friends my friends have is more than the number of my friends,'' mathematics and simulation It is explained in an easy-to-understand manner.
Your Friends Have More Friends Than You
In the first place, 'friends have more friends than you' is indicated by 'the average number of friends your friends have'. For example, let's say I have N friends. And the first friend has F 1 friends, the second friend has F 2 friends, and so on, and the nth friend has Fn friends. At this time, ``Average number of friends your friends have = [ F ]'' is expressed as ``(F 1 + F 2 + F 3 + ... + F N ) ÷ N''. So 'a friend has more friends than I do' can be expressed as '[ F ] exceeds N'.
According to Mr. Kemani, there are many cases where [ F ] exceeds N not only in real friendships but also in social networks such as Twitter and LinkedIn. Kemani uses a
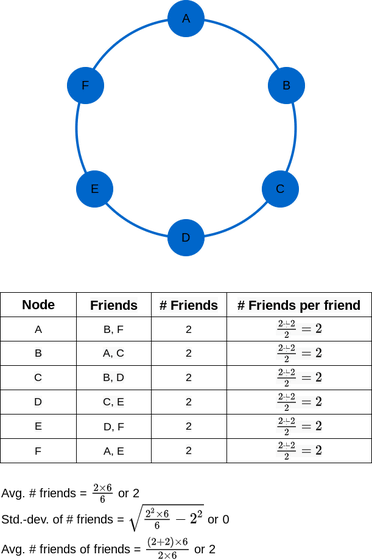
For example, below is an example of a network consisting of 6 people. The node parts with the letters A to F are individuals, and the edges connecting the nodes show friendships. Since each of the six people has two friends, the network can be said to be even, and the state at this time can be expressed as [ F ]=N.

But real networks are not even. Below is the addition of outlier nodes Z, which are connected to the above network much more than normal nodes. The number of friends of A to F, that is, N is 3 each, and only Z is 6. For A to F, the average number of friends that friends have, that is, [ F ] is (3 + 3 + 6) ÷ 3 = 4, and for A to F, [ F ] exceeds N. However, only Z, which is a highly connected node, does not have [ F ] greater than N.

In general, if there are f nodes in a network that are much more highly connected than other nodes, the remaining nodes 1-f in the network will have most connections than the nodes to which they are connected. is also less. Most real-world networks, especially social networks, have a small fraction of highly connected outlier nodes.
In one network, the average number of connections per node N is μ , and the standard deviation of the number of connections per node is σ. can do. Since μ and σ are positive real numbers, [ F ] is always greater than or equal to μ. Therefore, the average number of friends of friends is more than the number of own friends in most cases.
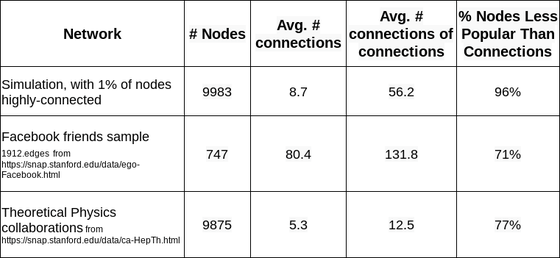
The table below is an example with three networks. From the top, the network is 'a network containing 1% of highly connected nodes', 'a part of Facebook's network', and 'network data used in previous research'. Nodes is 'number of nodes', Avg. #connections is 'average number of connections per node', Avg. #connections of connections is 'average number of connections of connected nodes', % Nodes Less Popular Than Connections is The percentage of nodes that fell below the average number of connections for a node. Looking at this table, in all networks, ``nodes whose average number of connections is less than the average number of connections of connected nodes'', that is, ``people who have more friends than themselves'' account for the majority of nodes. You can see that
By using this theory, it becomes possible to `` affect the diffusion of information exchanged locally between nodes connected within a certain network ''. In other words, knowing which nodes in the network are most strongly connected can be used to influence the spread of information.
For example, if you want to spread gossip to an entire network, rather than randomly picking members of the network and injecting gossip into them, you can have randomly chosen members pick friends and inject gossip into those friends. It will spread faster. Looking at the graph below, which summarizes the actual simulation results, you can see that the diffusion speed is faster in the latter method (red) than in the former method (blue).

Also, when detecting that an infectious disease is prevalent in a community, it is better to have randomly selected members monitor their friends (red) than randomly pick up members of the community and monitor them directly (blue). ) can detect infected people more quickly.

In addition, when the number of infected people is increasing rapidly like the new coronavirus, and there are only a limited number of vaccines, it is better to vaccinate randomly selected members from the community (blue). It is said that those who vaccinated friends who were randomly selected from our house (red) can suppress the increase in the number of infected people.

'Your friends are more likely to have more friends than you,' Kemani said. 'It might hurt, you might think it's impossible, or you might just feel weird. But it's true.' ' said.
Related Posts:
in Web Service, Science, Posted by log1i_yk