数学者も間違える確率の難問「モンティ・ホール問題」をイラストで解説

by palbo

モンティ・ホール問題は、高名な数学者まで間違えるほど「直感で正しいと思える解答と論理的に正しい解答が異なる問題」として有名な確率論の難問です。そんなモンティ・ホール問題について、イラストで視覚的に考え方を理解できる解説が公開されています。

Making the Monty Hall problem weirder but obvious - DYNO MIGHT
https://dyno-might.github.io/2020/09/17/making-the-monty-hall-problem-weirder-but-obvious/

モンティ・ホール問題は、以下のような問題です。

「プレーヤーの前に閉じた3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろには、はずれを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。プレーヤーが1つのドアを選択した後、司会のモンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。ここでプレーヤーは、最初に選んだドアを、残っている開けられていないドアに変更してもよいと言われる。ここでプレーヤーはドアを変更すべきだろうか？」

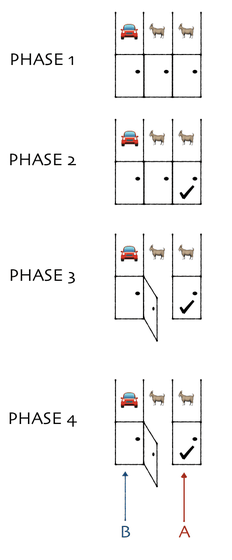
モンティ・ホール問題では、司会のモンティがドアを開けてヤギを見せた段階で残されたドアは2つなので、「2つ残されたドアのうち、それぞれのドアに新車が入っている確率は2分の1ずつ。どちらのドアを選んでも確率が変わらないのだから、ドアを変更してもしなくても状況は同じだ」と直感的に考えてがち。しかし、実際には「ドアを変更すると新車が得られる確率は3分の2で、変更しなければ3分の1」となり、「ドアを変更すべき」という答えが正解です。

この問題がアメリカのニュース雑誌「Parade」に回答付きで掲載されたところ、全米から「間違っている」という指摘が1万件以上も殺到。一連の議論に数学者まで参加し、ニューヨーク・タイムズなどの大手紙まで議論を掲載するという事態に発展しました。

科学的問題を論じるブログ「DYNO MIGHT」に掲載されたモンティ・ホール問題の解説は、「ドアを10枚として考えてみる」というもの。大本となったモンティ・ホール問題では「プレイヤーの前には閉じた3つのドアがあった」という設定ですが、これを「閉じた10枚のドアがあった」として考えます。

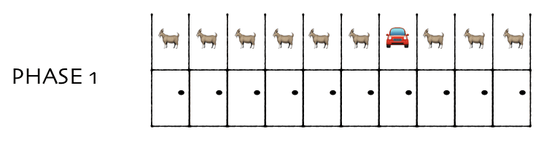
プレイヤーは、10枚のドアの中から1枚を選択します。

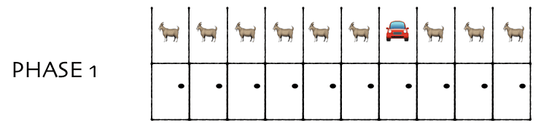
大本のゲームでは、ここで司会のモンティが外れのドアを開けます。しかし、今回はモンティが外れのドアを開ける代わりに、「最初に選んだドア以外の中身を全部獲得できる」と言ったと考えてみます。この場合、「最初に選んだドアの中身を獲得する」という選択で新車を入手できる確率は10％。「最初に選んだドア以外の中身を全部獲得できる」という選択で新車を入手できる確率は90％だと直感的に理解できます。

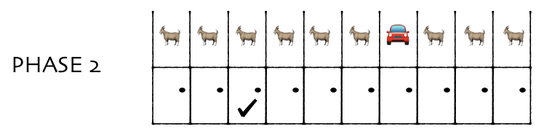
続いては、モンティが外れのドアを開けた上で、「最初に選んだドア以外の中身を全部獲得できる」という選択肢を提示するという例を見ていきます。まずはプレイヤーに10枚のドアが提示され……

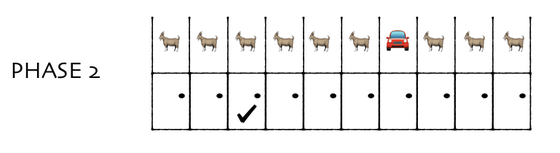
その中から1枚を選択するところまでは一緒。

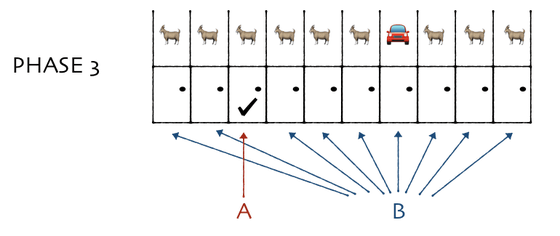
ここで、モンティが残された9枚のドアのうち、外れの8枚を開けるというのが相違点。

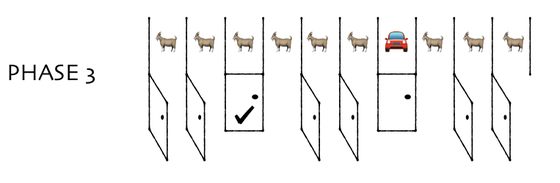
外れの8枚を開けたとしても、「最初に選んだドア以外の中身を全部獲得できる」ならば、90％の確率で新車を入手できることが視覚的に理解できます。

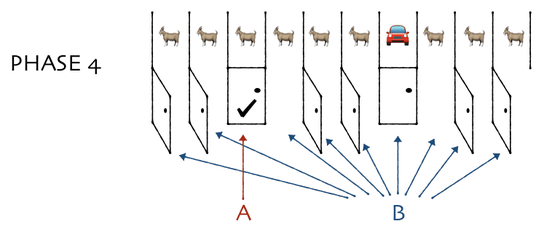
最後に、「最初に選んだドア以外の中身を全部獲得できる」という選択肢ではなく、「最初に選んだのとは別の閉じたドアの中身を獲得できる」という選択肢が提示される例を考えます。まずはプレイヤーに10枚のドアが提示されます。

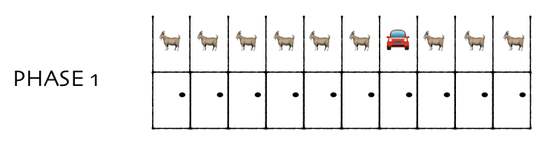
続いて、その中から1枚を選択。

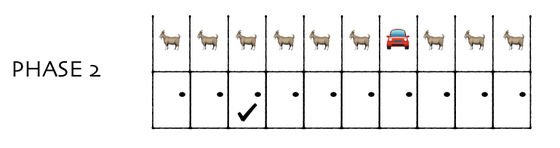
モンティが残った9枚のドアのうち、外れの8枚を開けます。

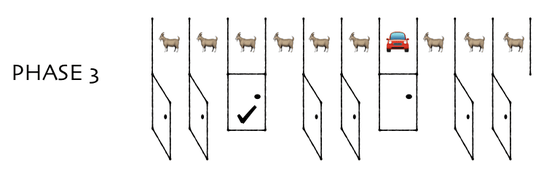
これまでの例では、「最初に選んだドア以外の中身を全部獲得できる」という選択について考えてきましたが、今回提示されたのは「最初に選んだのとは異なる閉じたドアの中身を獲得できる」という選択です。

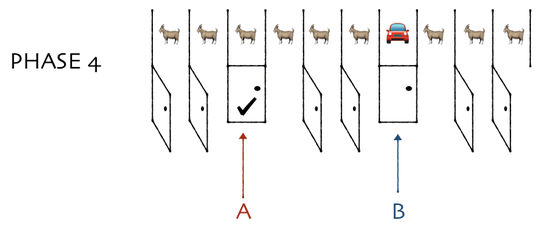
しかし、この2つの選択の差について着目すると、この2つの選択は「外れのドアの中身を獲得できるかどうか」だけが異なっており、「新車を獲得できるかどうか」については差は一切なく、「新車を獲得できる確率」には変化がありません。なので、「最初に選んだのとは異なる閉じたドアの中身を獲得できる」という選択肢を選んだとしても、新車を獲得できる確率は90％のままというわけです。

大本となったモンティ・ホール問題は、先ほどの例からドアの枚数を3枚にしただけ。ドアが3枚になったとしても考え方は共通なので、「ドアを変更する」という選択肢が正しいことがわかります。