トランプを1枚だけシャッフルすることを繰り返して「完全に混ざった状態」にできるのか？

「何度トランプをシャッフルしてもキレイに混ざらない」という状況を経験したことがある人も多いはず。ジョージア工科大学で機械学習やデータ駆動型システムのインターフェイス開発について取り組んでいるフレッド・ホーマン氏が、「トランプを1枚だけシャッフルして完全に混ざった状態にするためには、試行を何回繰り返す必要があるのか？」という疑問を独自に調査しています。

The Math of Card Shuffling
https://fredhohman.com/card-shuffling/

オーバーハンドシャッフルやリフルシャッフル、ヒンドゥーシャッフルなど、ひとくちに「シャッフル」といっても、さまざまな方法があります「どのシャッフルが効率的なのか」についての研究は多数行われており、2つに分けたカードを噛み合わせながら混ぜるリフルシャッフルでは、「7回」の試行でカードをランダムにできることが分かっています。

トランプのシャッフルにおける可視化と最適な組み合わせに関する検討
(PDFファイル)https://www.ipsj.or.jp/award/9faeag0000004f1r-att/CF-011.pdf

リフルシャッフルは、「52枚のトランプを半分(26枚ずつ)に分け、片方の組の間にもう片方の組をバラバラに挿入する」というシャッフル法です。今回ホーマン氏は、通常のリフルシャッフルを単純化して、「トランプを『1枚と51枚』に分割する」という特殊なリフルシャッフルについてシミュレーションを行いました。

実際にこの特殊なリフルシャッフルを行ってみます。初期状態では、スペード、クラブ、ハート、ダイヤの順にカードがA(1)からK(13)まで並んでいるとします。

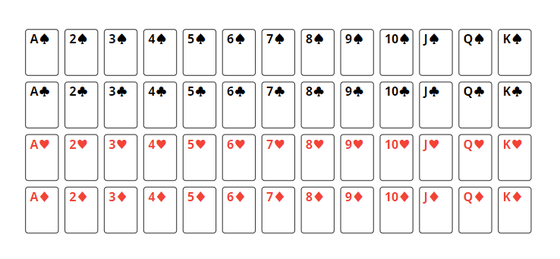
ホーマン氏が考えた特殊なリフルシャッフルは、「一番上のカード1枚を山札のどこかに入れる」というシャッフルです。初期状態ではスペードのAが一番上なので、試行を1回行うとスペードのAが山札のどこかに移動します。

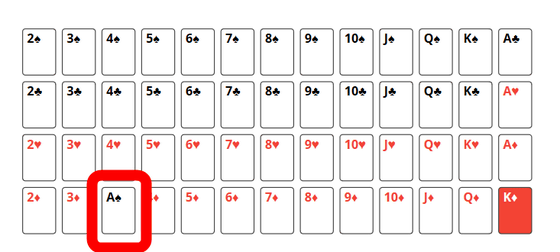
後はこれを繰り返して、「カードが全部混ざった状態」を目指します。今回ホーマン氏は、カードが全部混ざった状態を「最初に山札の底にあったダイヤのKが山札の一番上に来た状態」と定義。ダイヤのKが山札の一番上に来たならば、デッキ全体がよく混ざった状態になったとしています。

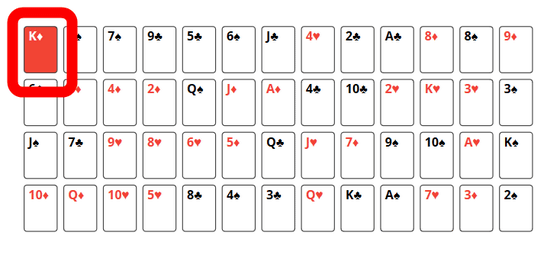
スタート時点でダイヤのKは山札の底。「一番上のカードをランダムに山札に入れる」という試行を行った場合、「ダイヤのKよりも上層にカードが入る」「ダイヤのKよりも下層にカードが入る」という2種類の結果が考えられます。上層にカードが入った場合にはダイヤのKの位置は変動しませんが、ダイヤのKよりも下層にカードが入った場合にはダイヤのKの位置は山札の中で1枚分上に来ます。

一番上のカードをランダムに山札に入れることを考える場合、カードが挿入される位置は「一番上」から「底」までの52通り存在します。ダイヤのKの位置が底だった場合、「ダイヤのKよりも下層にカードが入る」パターンは、底にカードが挿入される場合しかあり得ないので、確率は52分の1です。ダイヤのKが底から2番目だった場合、「ダイヤのKよりも下層にカードが入る」パターンは、底ないしはダイヤのKの真下にカードが挿入されるパターンの2通りなので、確率は52分の2です。

同様に、ダイヤのKの位置が下から数えて「i番目」だった場合、「ダイヤのKよりも下層にカードが入る」パターンの確率は、52分のiとなります。これらを踏まえてダイヤのKが一番上に来るまでの試行回数を計算すると、およそ236回になるとのこと。

ホーマン氏は、このシャッフルを実際に試行できるシミュレーターも公開しています。シミュレーターはこんな感じで、山札を上から順に並べた図と、試行を1回行う「Riffle」と試行を10回連続して行う「Riffle (x10)」という2つのボタンがあります。「Riffle」をクリックすると……

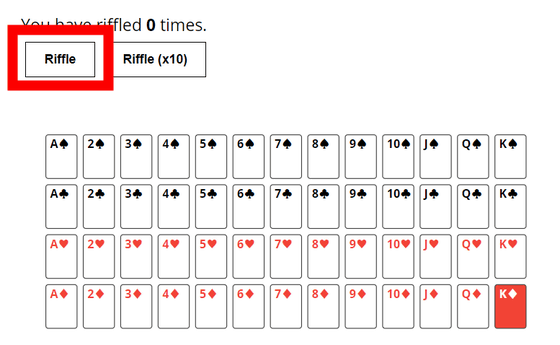
1回シャッフルされて、先頭のカードが山札のどこかに移動して、試行した総回数が記録されます。

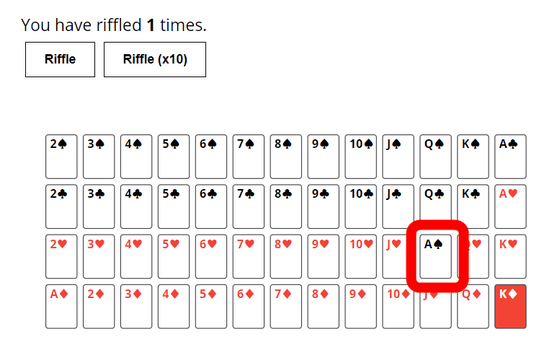
実際に試行を続けてみると、18回目でダイヤのKが一番下から移動。

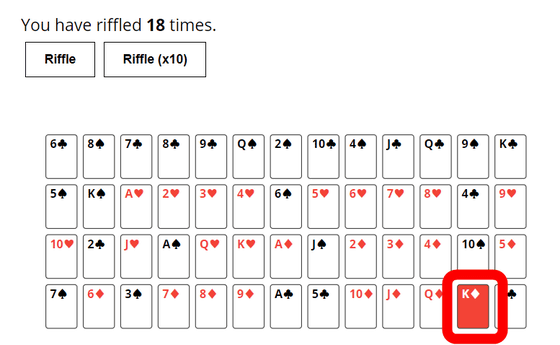
139回目でダイヤのKは山札の半分より上に。

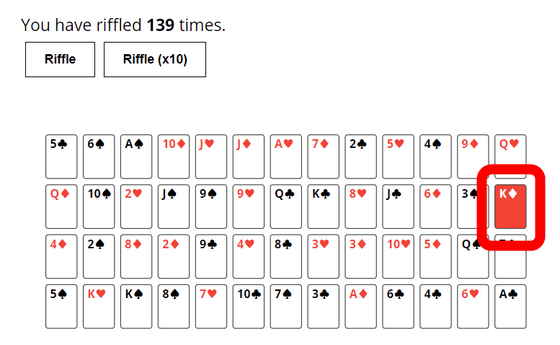
176回で山札の一番上に達しました。

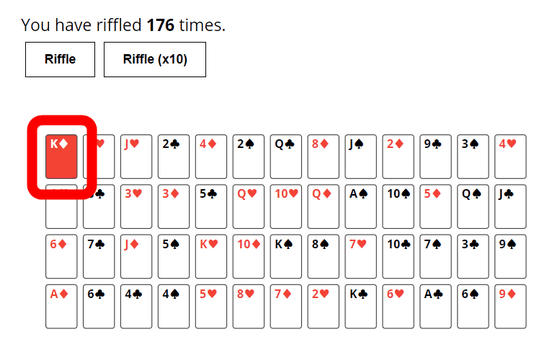
試行回数に応じたダイヤのKの位置をグラフで確認することもできます。

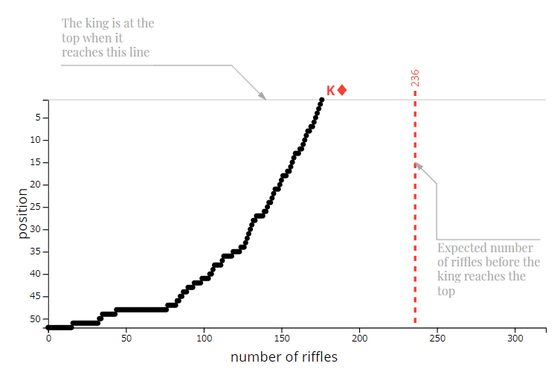
なお、世の中には「カードを机の上でかき混ぜる」という原始的なシャッフル方法の場合は何秒間で完璧に混ざった状態を作り上げられるのかを調査している数学者もいます。

「カードを机の上でかき混ぜたら何秒で完璧に混ざるのか？」にガチンコで挑む数学者がいる - GIGAZINE