Oct 09, 2020 07:00:00

Illustrations explain the difficult problem 'Monty Hall problem' that mathematicians can make mistakes

by

palbo

The Monty Hall problem is a difficult problem in probability theory that is so famous that even a well-known mathematician mistakes it as 'a problem in which the answer that seems intuitively correct and the answer that is logically correct are different'. An explanation of the Monty Hall problem that allows you to visually understand the idea with illustrations has been released.

Making the Monty Hall problem weirder but obvious --DYNO MIGHT
https://dyno-might.github.io/2020/09/17/making-the-monty-hall-problem-weirder-but-obvious/

The Monty Hall problem is as follows.

'There are three closed doors in front of the player, behind one door there is a new prize car, and behind the two doors there is a goat, which means out of place. When the player hits the door of the new car You will get a new car. After the player chooses one door, the moderator Monty opens the remaining door with the goat and shows the goat. Here the player opens the first door he chooses with the remaining open. It is said that the door may be changed to an unopened door. Should the player change the door here? '

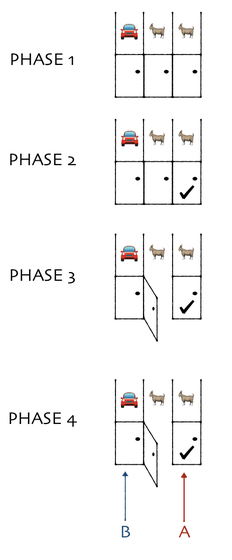
In the Monty Hall problem, there are two doors left when the moderator Monty opens the door and shows the goat, so 'Of the two doors left, the probability that each door has a new car is It's a half each. The probability is the same no matter which door you choose, so the situation is the same whether you change the door or not. ' However, in reality, 'the probability of getting a new car by changing the door is two-thirds, and if you do not change it, it is one-third', and the correct answer is 'you should change the door'.

When this problem was published in the American news magazine 'Parade' with an answer, more than 10,000 cases were flooded with 'wrong' points from all over the United States. Even mathematicians participated in a series of discussions, and even large letters such as the New York Times posted the discussions.

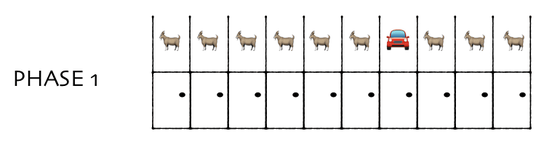
The explanation of the Monty Hall problem published in the blog 'DYNO MIGHT' that discusses scientific problems is 'Think of 10 doors.' In the Monty Hall problem, which became the main story, the setting was 'there were three closed doors in front of the player', but we think of this as 'there were ten closed doors'.

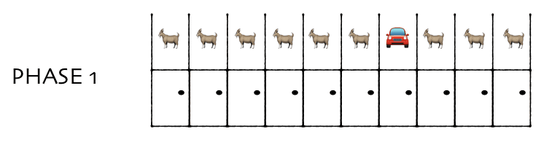
The player chooses one of the ten doors.

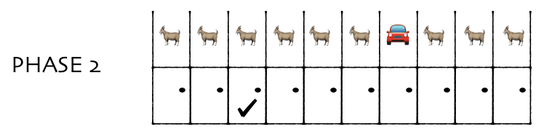
In the main game, the moderator Monty opens the door here. But this time, instead of opening the door, Monty said, 'You can get everything except the first door you chose .' In this case, there is a 10% chance that you will get a new car by choosing 'Get the contents of the door you chose first'. You can intuitively understand that the probability of getting a new car is 90% by selecting 'You can get all the contents except the door you chose first'.

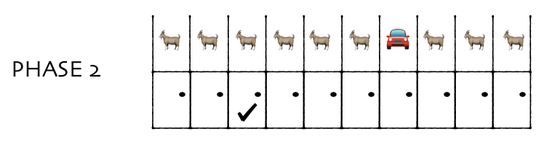
Next, let's look at an example in which Monty opens the door and presents the option of 'getting all the contents except the first door you chose.' First of all, 10 doors are presented to the player ...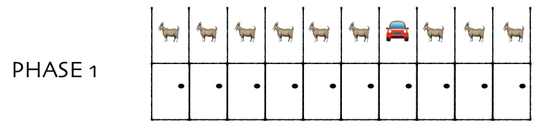

It is the same up to the point of selecting one from them.

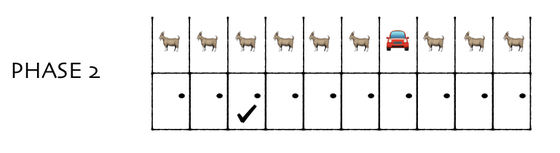
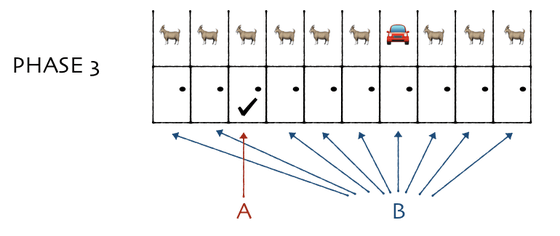
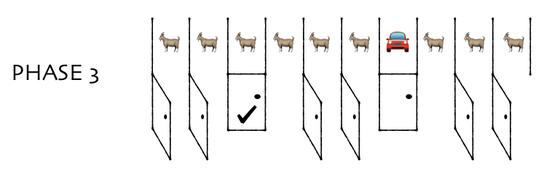
The difference here is that of the nine doors that Monty has left, eight of the doors that come off are opened.

Even if you open the 8 outliers, you can visually understand that you can get a new car with a 90% chance if you can 'acquire all the contents except the door you chose first'.

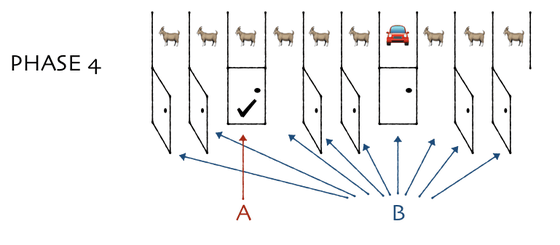
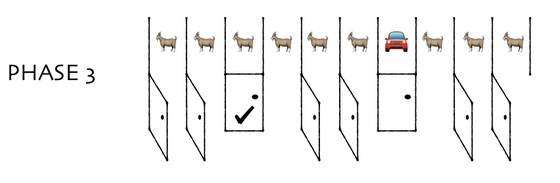
Finally, consider an example in which the option 'You can get the contents of a closed door different from the one you chose first ' is presented instead of the option 'You can get all the contents other than the first selected door '. I will. First, the player will be presented with 10 doors.

Then, select one from them.

Open the 8 out of the 9 doors where Monty remains.

In the examples so far, we have considered the choice of 'getting all the contents other than the door you chose first', but this time we presented 'the contents of a closed door different from the one you chose first'. You can get it. '

However, focusing on the difference between these two choices, the two choices differ only in 'whether or not they can acquire the contents of the out-of-door', and there is no difference in 'whether or not they can acquire a new car'. There is no change in the 'probability of getting a new car'. So, even if you choose the option 'You can get the contents of a closed door different from the one you chose first', the probability of getting a new car remains 90%.

The problem with the Monty Hall problem, which became a major issue, was just to reduce the number of doors to three from the previous example. Even if there are three doors, the idea is the same, so you can see that the option to 'change the door' is correct.