An easy-to-understand explanation of the probability problem 'Monty Hall problem' to find a hit from three boxes is like this

The ' Monty Hall problem ' is one of the probability problems that is known for being difficult to understand even when the result is explained. Engineer Mikhail Paszkiewicz explains how to explain the Monty Hall problem to people who don't understand it, and has released a demo where you can actually experience it.
Monty Hall explained
https://www.michalpaszkiewicz.co.uk/blog/montyhallexplained/index.html
The Monty Hall problem is a great example of how mathematics seems to be inconsistent with common sense, and was first posed by Steve Selvin in a letter to an American statistician in 1975. This problem was picked up by the American television program ``Let's Make a Deal,'' and it became known as the Monty Hall problem, named after the show's host, Monty Hall.
Here's what the Monty Hall problem is:
Three boxes labeled A, B, and C are prepared in the field, and the person who challenges the problem chooses one of them. One of the three boxes is a hit, but the remaining two are losers.

Afterwards, the questioner who knows which box contains the winning box will reveal that one of the three boxes is a losing box.

Next, the challenger chooses the winning box from the remaining boxes. At this time, the challenger may choose the box they originally selected, or they may change to a different box. After that, the winning box will be revealed.

The strange thing about this problem is that the probability of winning increases if you change the box you originally selected to something else. Most people intuitively think that the probability of winning is 1/2 (50%) because they ultimately choose the box that contains the winning box from two boxes.
However, it has been found that if you select a box first and then switch to another box after the losing box is revealed, the probability of drawing a win increases to 66.6%. For those who don't know that ``If you change the first box you choose, the probability of winning increases to 66.6%'', the table below summarizes all the options. You can clearly see that the probability of winning is 6/9 (2/3 or 66.6%).
| winning box | challenger first the chosen box | The questioner revealed box of losers | The challenger takes the box When changing | result |
|---|---|---|---|---|
| A | A | B or C | A to B or C | Loser |
| A | B | C | B to A | Hit |
| A | C | B | C to A | Hit |
| B | A | C | A to B | Hit |
| B | B | A or C | B to A or C | Loser |
| B | C | A | C to B | Hit |
| C | A | B | A to C | Hit |
| C | B | A | B to C | Hit |
| C | C | A or B | C to A or B | Loser |
In the first place, the probability that any of the three boxes contains a hit is 1/3 (33.3%), so the probability that the remaining boxes contain a hit is 2/3 (66.6%). Therefore, before the questioner reveals the losing box, it can be determined that choosing a box other than the one originally selected has a higher probability of winning.
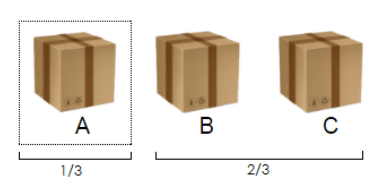
In the first place, even if the questioner reveals one losing box, there is actually no effect. This is because the probability of winning the first box is 1/3 (33.3%), which is the same as the first box.
In his article, Paszkiewicz presents a game that allows you to experience the Monty Hall problem. You can play in the area where the cards are lined up at the bottom of the linked page.
Monty Hall explained
https://www.michalpaszkiewicz.co.uk/blog/montyhallexplained/index.html
The Pacman card is a win, and the monster card is a loss. When you actually play the game, you will realize that the probability of winning is higher if you choose a card first and choose another card after the loss is revealed.
This is what it looks like when you experience the 'Monty Hall problem' - YouTube
Even easier to understand is when you increase the number of cards to 20 (1 winning, 19 losing) and play the game with the same rules. In this case, the questioner will disclose 18 missing cards. Then, the probability that the first card selected will be a hit is 1/20 (5%), and the probability that the other cards will be a hit is 19/20 (95%). Therefore, if you choose a card different from the first card you chose, the probability of drawing a hit is 19/20 (95%), which is overwhelmingly high.

Related Posts: