証明されれば素数の謎を解明する鍵となる懸賞金100万ドルの難問「リーマン予想」とはどういう問題なのか？

アメリカのクレイ数学研究所によって2000年に発表された、100万ドル(約1億6000万円)の懸賞金がかけられている問題が「ミレニアム懸賞問題」です。このうちの1つであるリーマン予想は「素数の分布」に関する問題として特に有名で、160年以上も世界中の数学者を悩ませています。

The Riemann Hypothesis, the Biggest Problem in Mathematics, Is a Step Closer to Being Solved | Scientific American
https://www.scientificamerican.com/article/the-riemann-hypothesis-the-biggest-problem-in-mathematics-is-a-step-closer/

リーマン予想がどういう問題なのかについては、科学系メディアのQuanta Magazineが以下のムービーで解説しています。

The Riemann Hypothesis, Explained - YouTube

素数とは「1とその数でしか割り切れない自然数」のことです。紀元前3世紀頃、古代ギリシャの数学者であるユークリッドは、素数が無限に存在することを証明しました。

そんな素数の魅力に取りつかれたのが、18世紀～19世紀に活躍したドイツの大数学者であるカール・フリードリヒ・ガウスでした。ガウスは10代の頃に素数を300万個も書き出し、表にまとめています。

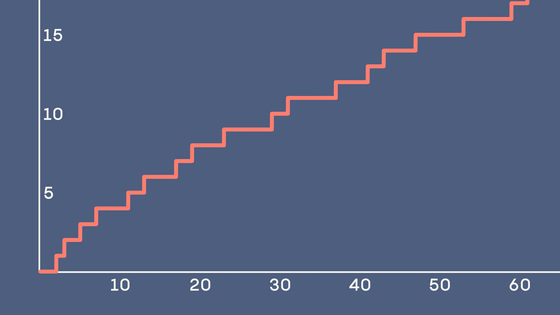
そして、ガウスは「素数計数関数」の研究を行いました。素数計数関数とは文字通り、自然数nに対して、n以下の素数の個数を数える関数です。以下は、縦軸を素数計数関数π(n)、横軸をnとしてグラフにしたもの。素数の個数は1ずつ増えていくため、π(n)のグラフはまるで階段のような形状をしています

しかし、nの上限をずっと大きく取ると、グラフは以下のように1本のなだらかな線のように見えます。

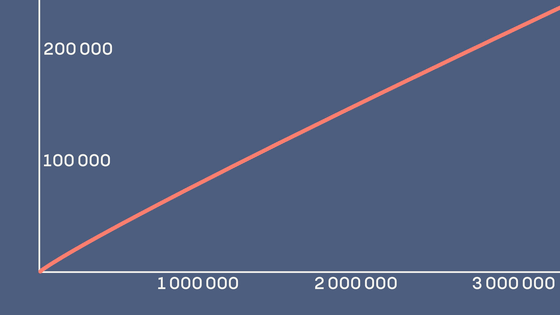
ガウスはこのπ(n)が、対数積分関数という関数にかなり近いということを発見しました。つまり、自然数の中に素数がどのくらいの割合で含まれているかを、対数を使って近似できるというわけです。これがガウスの素数定理です。

そして、時代はガウスが活躍した頃から少しさかのぼり、18世紀前半に活躍した数学者のレオンハルト・オイラーの業績に注目。

オイラーが残した数学的業績は偉大かつ膨大ですが、その中の1つに「無限級数の追究」があります。無限級数とは無限に続く数列の和のことです。

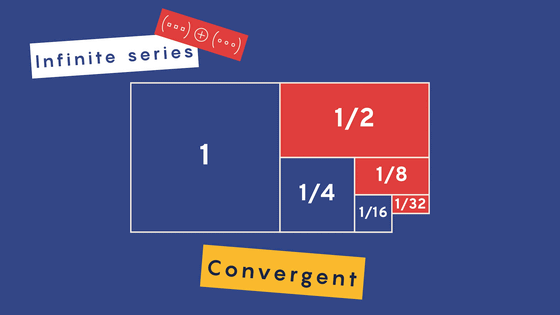
例えば、1/xの無限級数は1/1＋1/2＋1/3＋1/4＋……と表わされます。この1/xの無限級数は発散、すなわち有限値に収束しないことが証明されています。

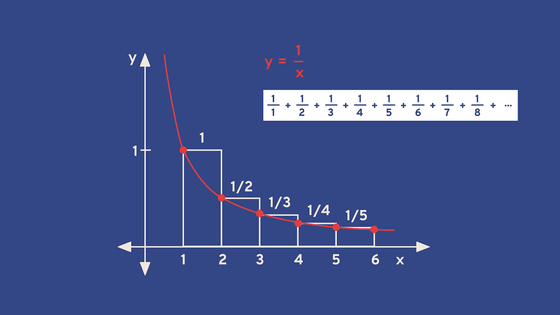
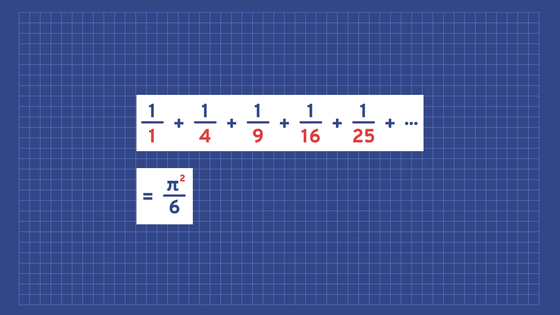
しかし、1/x²の無限級数はなんとπ²/6に収束することをオイラーは突き止めました。さらに、オイラーは1/x⁴の無限級数がπ⁴/90に収束することも証明しています。

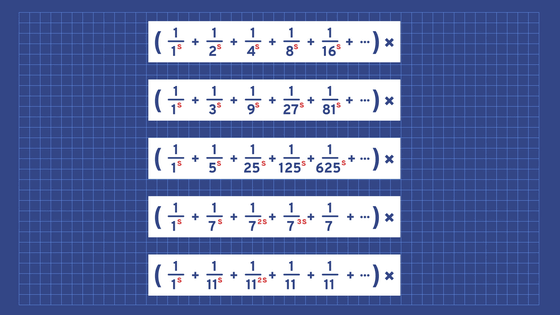
これらの無限級数を一般化し、1/x^sの無限級数＝1/1^s＋1/2^s＋1/3^s＋1/4^s＋……で表わされる関数ζ(s)が「ゼータ関数」です。

オイラーは、このゼータ関数が素数を使った積で表現できることを発見しました。これをオイラー積と呼びます。

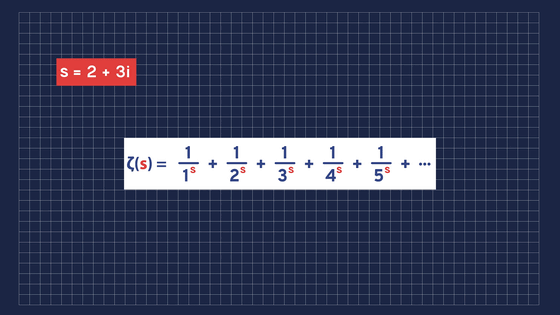
素数とゼータ関数のつながりが見えたところで登場するのが、ガウスの弟子でもあるドイツの数学者、ベルンハルト・リーマンです。リーマンは、このゼータ関数に複素解析の考え方を導入しました。

複素解析とは「複素数」を関数に導入する考え方。複素数は、2乗したら-1になる数＝iを単位とする虚数と実数で表現される数のことで、複素数を「x+yi」という形で示した時、実数部分(実部)はx、虚数部分(虚部)はyとなります。

ζ(s)は、x＞1であればらせんを描きながら有限値に収束します。

x＞1の時、sに対するζ(s)を複素数平面上に表現した等角写像が以下の右側の青い部分です。

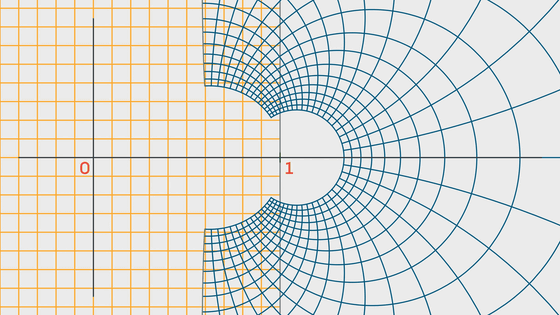
リーマンは「解析接続」という手法でζ(s)の定義域を広げ、x＜1におけるζ(s)も考えました。

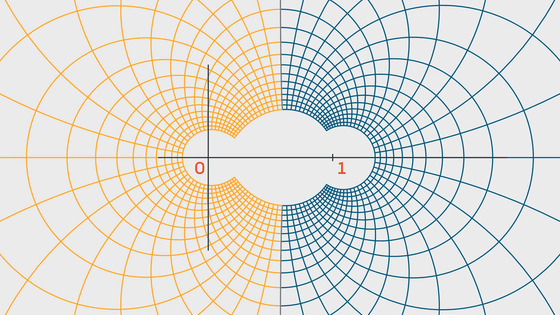
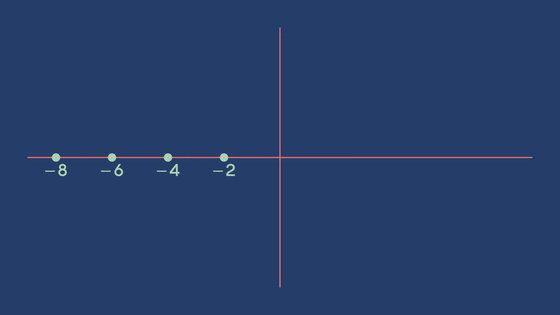
この時、sが-2、-4、-6……という負の偶数である場合、ζ(s)＝0となります。このことは容易に証明可能であることから、負の偶数となるsは「自明な零点」と呼ばれます。

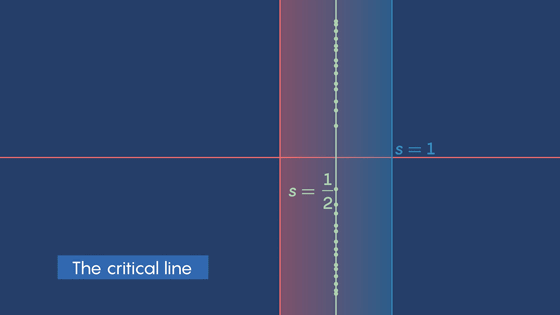
さらに、ζ(s)＝0となるようなsは、0＜x＜1の範囲にも無限個存在することがわかりました。このsは「非自明な零点」と呼ばれます。リーマンは「非自明な零点はx＝1/2のライン上にしか存在しない」と予想しました。これこそがリーマン予想です。

ここで、ガウスが考えた素数定理に話を戻します。ガウスが提唱した素数定理は「素数の個数を示す素数計数関数と対数積分関数がかなり近い」ことを示していますが、「近い」ということは必ず誤差があります。リーマンは、1859年に発表した論文「与えられた数より小さい素数の個数について」で、ゼータ関数の零点を使うことで素数計数関数をより精密に表現できると考えました。つまり、リーマン予想が証明されれば、素数の分布を極めて高い精度で求めることができるようになるわけです。

しかし、予想を提示したリーマン自身は「非自明な零点がx＝1/2上にしか存在しない」という予想について、「厳密に証明されることが望ましいが、自分で証明を試みたものの成果が得られなかったため、さしあたって証明はしていない」と論文に記しました。

コンピューターが進歩して膨大な計算を高速で行えるようになってから、実際にζ(s)となるような複素数sが10兆個も検証されました。その結果、検証した非自明な零点はすべてx＝1/2を満たすことがわかりました。コンピューターの圧倒的な計算力で強引に非自明な零点を見つけているわけですが、万が一、x＝1/2ではない非自明な零点が発見されれば、その時点でリーマン予想は誤りであったことになります。この方法ではリーマン予想が間違っていたことを示すことはできても、リーマン予想が正しいことは証明できません。

数学者は160年以上にわたってリーマン予想に挑戦していますが、いまだに解決には至っていません。そこで、「1/2＜x＜1となるようなsにおいて、非自明な零点がN個あると仮定し、このNを0に近づけていく」というアプローチが取られましたが、イギリスの数学者であるアルバート・インガムが1940年に発表した論文から現代に至るまでほぼ進展していませんでした。

2024年5月末、マサチューセッツ工科大学の数学者であるラリー・ガス氏とオックスフォード大学のジェームズ・メイナード氏が、80年越しにインガムの研究結果からさらに一歩進むことに成功したと主張する論文を未査読論文リポジトリのarXivに掲載しました。著名な数学者であるテレンス・タオ氏はMastodonで、「リーマン予想に向けて目覚ましい進歩がありました。この予想を完全に解決するにはまだほど遠いですが」とコメントしています。