What is the 'Riemann Hypothesis,' a difficult problem with a $1 million prize that, if proven, will solve the mystery of prime numbers?



The Millennium Prize Problems , announced in 2000 by the Clay Mathematics Institute in the United States, are problems with a prize of $1 million (approximately 160 million yen). One of these problems , the Riemann hypothesis , is particularly famous as a problem about the distribution of prime numbers, and has been troubling mathematicians around the world for over 160 years.

The Riemann Hypothesis, the Biggest Problem in Mathematics, Is a Step Closer to Being Solved | Scientific American
https://www.scientificamerican.com/article/the-riemann-hypothesis-the-biggest-problem-in-mathematics-is-a-step-closer/

The science media Quanta Magazine explains what the Riemann hypothesis is in the following movie.

The Riemann Hypothesis, Explained - YouTube


A prime number is a natural number that can only be divisible by 1 and itself. Around the 3rd century BC, the ancient Greek mathematician Euclid proved that there are an infinite number of prime numbers .



The great German mathematician

Carl Friedrich Gauss, who was active in the 18th and 19th centuries, was fascinated by prime numbers. When he was a teenager, Gauss wrote out 3 million prime numbers and compiled them in a table.



Gauss then researched the '

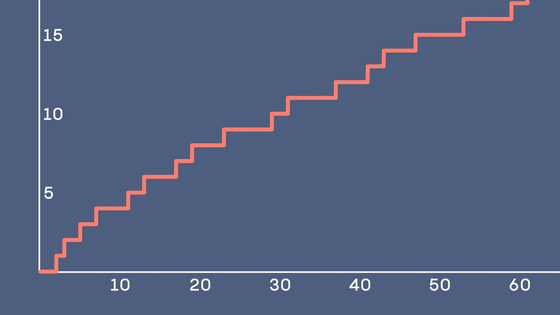
prime counting function .' The prime counting function is, as the name suggests, a function that counts the number of prime numbers less than or equal to a natural number, n. Below is a graph with the prime counting function π(n) on the vertical axis and n on the horizontal axis. Because the number of prime numbers increases by 1, the graph of π(n) looks like a staircase.



However, if we choose a much larger upper limit for n, the graph will look like a single smooth line, like this:



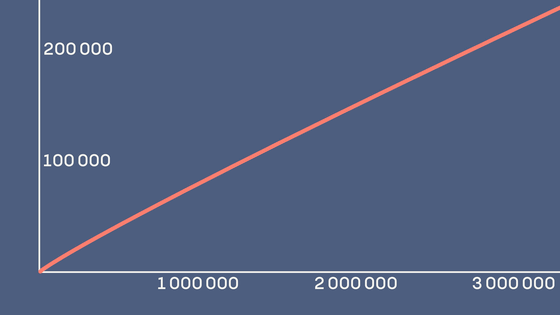
Gauss discovered that π(n) is very close to a function called the logarithmic integral function . In other words, it is possible to approximate the percentage of prime numbers among natural numbers using logarithms. This is Gauss's Prime Number Theorem .



Next, let's go back a little in time from Gauss's time and look at the achievements of

Leonhard Euler, a mathematician who was active in the first half of the 18th century.



Euler left behind many great and numerous mathematical achievements, one of which was his 'investigation of infinite series.' An infinite series is the sum of a sequence of numbers that continues infinitely.



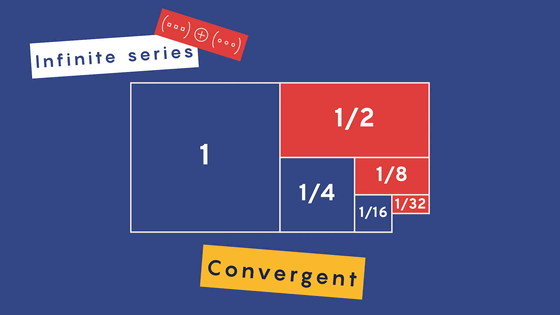
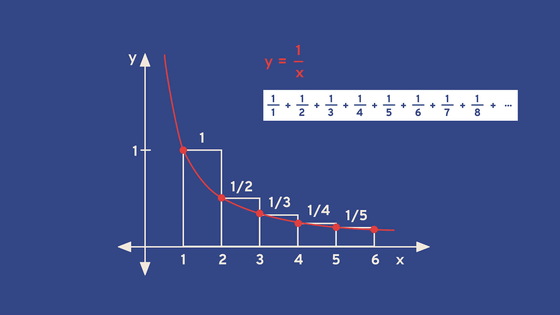
For example, the infinite series of 1/x can be expressed as 1/1 + 1/2 + 1/3 + 1/4 + .... It has been proven that this infinite series of 1/x

diverges , that is, it does not converge to a finite value.



However, Euler discovered that the infinite series of 1/x 2 converges to an amazing π 2 /6. Furthermore, Euler proved that the infinite series of 1/x 4 converges to π 4 /90.



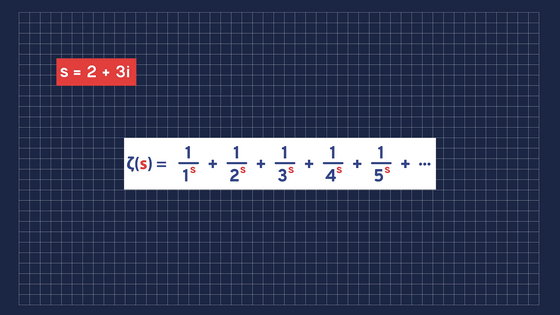
Generalizing these infinite series, the function ζ(s) expressed as the infinite series of 1/x s = 1/1 s + 1/2 s + 1/3 s + 1/4 s +…… is the 'Zeta function.'



Euler discovered that the zeta function can be expressed as a product of prime numbers, called

the Euler product .



Now that we have seen the connection between prime numbers and the Zeta function, the German mathematician and student of Gauss,

Bernhard Riemann, comes on the scene. Riemann introduced the idea of complex analysis to the Zeta function.



Complex analysis is the idea of introducing '

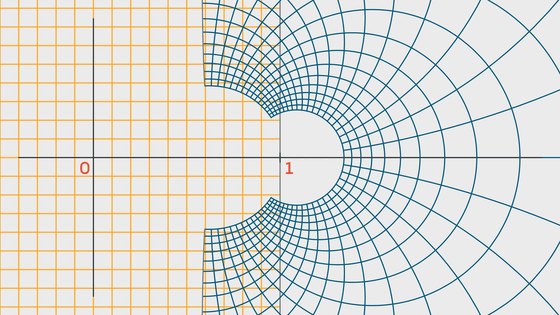
complex numbers ' into functions. Complex numbers are numbers expressed as real and imaginary numbers, with i as the unit, which becomes -1 when squared. When a complex number is expressed in the form 'x+yi', the real part is x and the imaginary part is y.



ζ(s) converges to a finite value in a spiral fashion if x]1.



When x]1,

the conformal mapping of ζ(s) with respect to s on the complex plane is shown in blue on the right side below.



Riemann expanded the domain of definition of ζ(s) using a technique called '

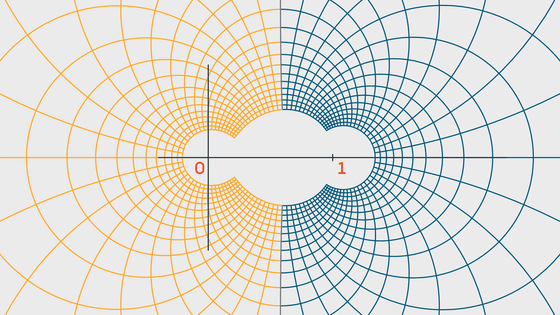
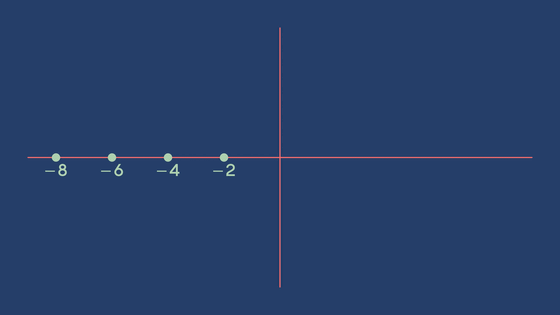
analytic continuation ', and also considered ζ(s) in x[1.



In this case, if s is a negative even number such as -2, -4, -6, etc., then ζ(s) = 0. Since this is easy to prove, negative even numbers s are called 'trivial zeros.'



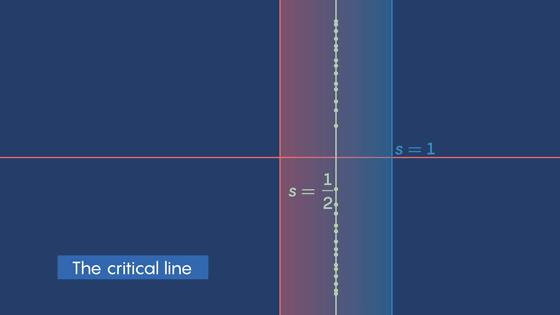
Furthermore, we found that there are an infinite number of s's in the range 0[x[1 such that ζ(s)＝0. These s's are called 'non-trivial zeros.' Riemann predicted that 'non-trivial zeros exist only on the line x＝1/2.' This is the Riemann hypothesis.



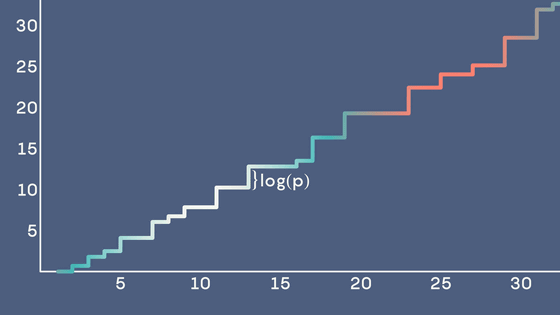
Let's go back to the prime number theorem devised by Gauss. The prime number theorem proposed by Gauss shows that 'the prime counting function, which indicates the number of prime numbers, and the logarithmic integral function are quite close,' but 'close' always means there is an error. In his paper 'On the Number of Primes Less Than a Given Number' published in 1859, Riemann thought that the prime counting function could be expressed more precisely by using the zeros of the zeta function. In other words, if the Riemann hypothesis is proven, it will be possible to calculate the distribution of prime numbers with extremely high accuracy.



However, Riemann himself, who proposed the conjecture, wrote in his paper that regarding the conjecture that 'non-trivial zero points exist only at x = 1/2,' 'It would be desirable for it to be proven rigorously, but since I have attempted to prove it myself but have not been successful, I have not given it a proof for the time being.'

As computers have advanced and become capable of performing massive calculations at high speed, 10 trillion complex numbers s that actually satisfy ζ(s) have been verified. As a result, it was found that all of the nontrivial zero points verified satisfy x = 1/2. Nontrivial zero points are forcibly found using the overwhelming computing power of computers, but if a nontrivial zero point other than x = 1/2 is discovered, then at that point the Riemann hypothesis would be incorrect. This method can show that the Riemann hypothesis is incorrect, but it cannot prove that it is correct.



Mathematicians have been trying to solve the Riemann hypothesis for over 160 years, but have yet to come up with a solution. So, the approach taken was to assume that there are N nontrivial zeros in s such that 1/2[x[1, and try to make N approach 0. However, there has been little progress on this since the British mathematician Albert Ingham published

a paper in 1940.

At the end of May 2024, Larry Gass, a mathematician at the Massachusetts Institute of Technology, and James Maynard of the University of Oxford published a paper on the unpeer-reviewed paper repository arXiv , claiming that after 80 years they had succeeded in going one step further than Ingham's research. Renowned mathematician Terence Tao commented on Mastodon, 'We have made remarkable progress toward the Riemann hypothesis, although we are still far from fully resolving it.'

Related Posts:

in Science,   Video, Posted by log1i_yk