Apr 10, 2023 14:30:00

A teenage girl shows a new proof of the Pythagorean theorem, rated as 'the most beautiful proof'

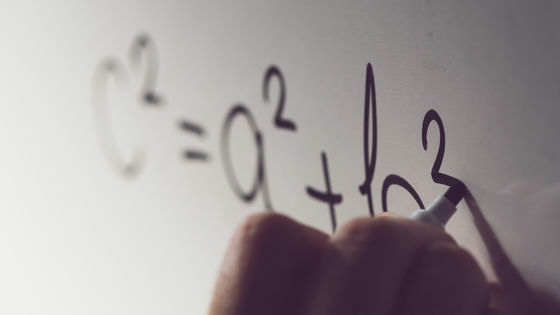
At the American Mathematical Society, two teenage girls presented a new proof of

the Pythagorean theorem . Keith McNulty, an expert in applied mathematics, said: 'It's a wonderful demonstration that excellence in a field of research is achievable by anyone with joy and passion, regardless of gender, ethnicity or sociodemographic background. In addition to describing it as an event, the proof method itself is causing ripples.

Here's How Two New Orleans Teenagers Found a New Proof of the Pythagorean Theorem | by Keith McNulty | Apr, 2023 | Medium
https://keith-mcnulty.medium.com/heres-how-two-new-orleans-teenagers-found-a-new-proof-of-the-pythagorean-theorem-b4f6e7e9ea2d

Two teenage girls from New Orleans, Louisiana, Carcia Johnson and Nekiya Jackson, presented to the American Mathematical Society (AMS) a new proof of the Pythagorean theorem. rice field. Both were students, and because the characteristics of African-American women were diametrically opposed to the mathematics society's majority population, McNulty said, 'Excellence in your chosen field of study is something that anyone can achieve.' It's a great reminder that something is always possible,' he said.

Also, according to Mr. McNulty, there was a big reason why this presentation created a big topic, and the proof method itself was what made eminent mathematicians even.

The Pythagorean theorem states that if we know the length of two sides of a right-angled triangle, ^we can calculate the ^length of the other ^side . is represented by the formula In Japan, it is a mathematical formula that is learned in junior high school as 'Pythagorean theorem', but hundreds of different patterns are shown in the proof of the mathematical formula.

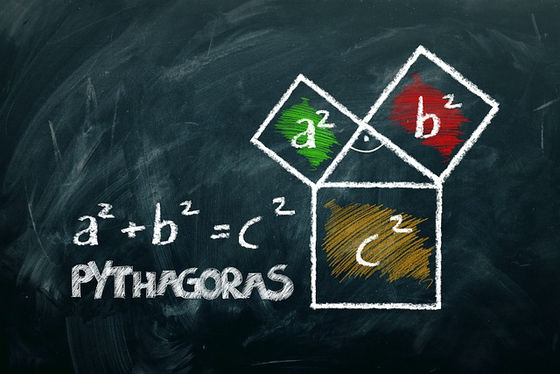
McNulty points out that the use of '

trigonometry' to prove this Pythagorean theorem had a big impact on the mathematical society. Trigonometry is an academic field that applies the relationship between the size of the angles and the lengths of the sides of a triangle to other studies such as proofs and surveys, but trigonometry itself depends on the Pythagorean theorem. Therefore, proving the Pythagorean theorem by trigonometry was considered to be 'impossible to prove the Pythagorean theorem by trigonometry' because it was a so-called circular reasoning that 'put the conclusion in the premise'.

However, according to McNulty, the viewpoint that 'the Pythagorean theorem cannot be proved by trigonometry' has been questioned in many cases in recent decades, and proof has been attempted many times. So while Johnson and Jackson's proof is not 'the first trigonometry proof of the Pythagorean theorem,' McNulty calls their proof 'the most beautiful and simplest trigonometry I have ever seen.' There is a possibility that it is a proof of '.' Together, McNulty says this is a job done by a young and sharp intellect, and an interesting phenomenon that defines the characteristics of many experienced mathematicians.

McNulty shows a new proof of the Pythagorean theorem using trigonometry in a diagram like the image below. In the figure, for a right-angled triangle with sides a, b, and c assuming 'a≠b', the angle between sides b and c is α, and the angle between sides a and c is β. For this right-angled triangle, ``1, form a horizontally inverted copy about side b'', ``2, extend straight line A perpendicular to side c from angle β'', and then ``3, straight line A and side Draw a straight line C that connects c”. Then, a large right-angled triangle is formed, in which you can draw infinitely smaller right-angled triangles that are similar to the original right-angled triangle from the upper left. Using this 'infinite sequence of similar triangles' to derive the lengths of lines A and C is the proof of Mr. Johnson and Mr. Jackson.

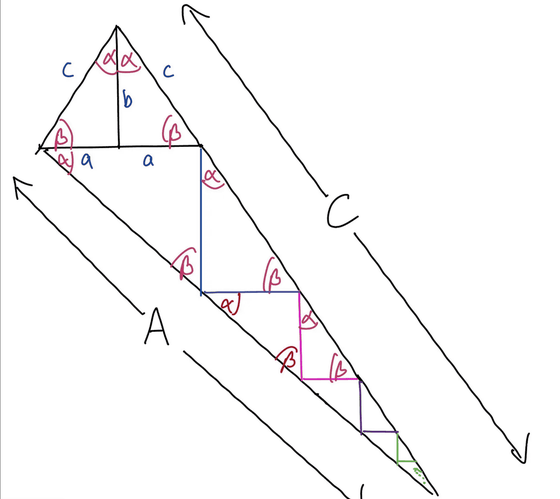
As shown in the figure, one side of the third triangle is represented by 2a, and using the trigonometric ratios ``sinα=cosβ=a/c'' and ``cosα=sinβ=b/c'', its hypotenuse is It can be expressed as '2a/sinβ=2ac/b'. In this way, an infinite number of similar triangles can be expressed using trigonometric ratios from the sides of adjacent triangles. At this time, the length of side A of the entire similar triangle is the sum of the geometric series of the first term '(2ac)/b' and the common ratio 'a ² /b ² ', which can be shown as follows.

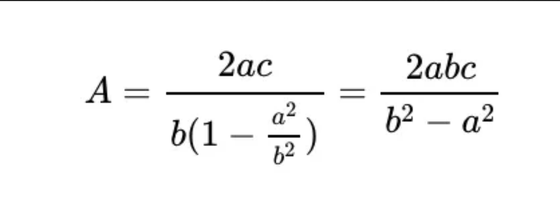
Similarly, straight line C is a geometric series with the first term '(2a ² c)/b ² ' and the common ratio 'a ² /b ² ', and is shown as follows.

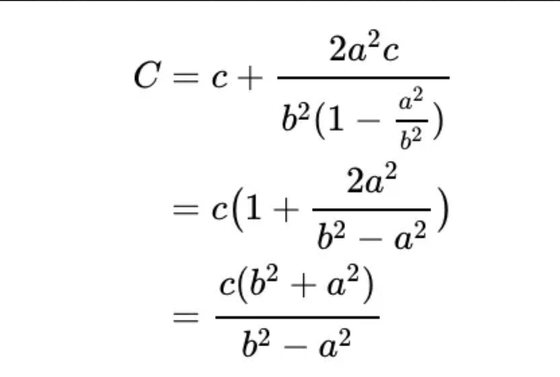
Calculating the ratio of A and C shown here is as follows, and in the trigonometric function, it is shown as 'opposite side / hypotenuse of sinθ = θ', so from the original figure, 'straight line A/C = sin(2α) I understand that it is.

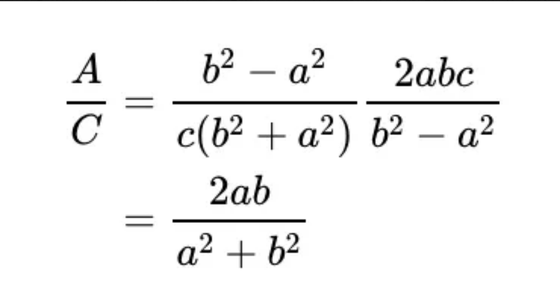
In addition, by copying the right-angled triangle horizontally at the very beginning of the original figure, one triangle that combines two right-angled triangles is an isosceles triangle. Here, if we use the sine theorem, which does not use the Pythagorean theorem , to convert the formula for the ratio of straight lines A and C, we end up with the following formula. Since a, b, and c are all non-zero, if the numerator is the same, the denominator should be the same. Therefore, 'a ² +b ² =c ² ' is given.

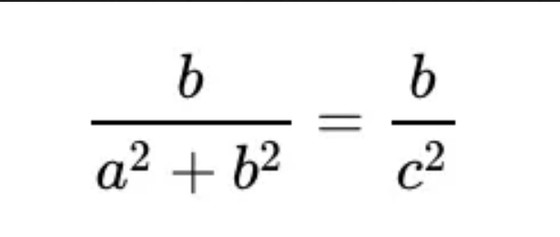
Hacker News also talked about this proof, saying, ``This proof only assumes that sine and cosine exist as ratios of the sides of the triangle, and the phrase that trigonometry is used is a misleading expression.'' On the other hand, there is a conventional belief that the law of sine cannot be used to prove it, and therefore it is considered impossible to prove the Pythagorean theorem using trigonometry, or sine or cosine. I think it was called a creative and unexpected proof because it was broken,' said one commenter , explaining what was groundbreaking about Johnson and Jackson's proof.

Also, regarding the fact that the proof by two African-American girls from the South, which is rarely seen in mathematics circles, aroused astonishment, the discussion included the opinion that academics should not be hindered by social backgrounds. ``Their proof is undoubtedly a great achievement, but McNulty's article does not mention that they attended a prestigious private high school. I think it's problematic to tell a story like 'Achievement from hard-to-reach areas'.'