The possibility that historical chess puzzle problem leads to elucidation of unresolved problems in modern mathematics

The board game "Chess" which has a history exceeding 1000 years is not mere game outcome but the various puzzle challenges that conform to that rule "Chess · problem"Is present.Eight QueenIt is a puzzle that uses only 8 queen out of chess pieces, but if you expand the scale greatly, it is an unresolved problem in modern mathematics and it will cost 100 million yen prize "P versus NP problemIt is considered to lead to the elucidation of.

2017 | "Simple" chess puzzle holds key to $ 1m prize | University of St Andrews
https://www.st-andrews.ac.uk/news/archive/2017/title,1539813,en.php

Can You Solve the Million-Dollar, Unsolvable Chess Problem? - Atlas Obscura
http://www.atlasobscura.com/articles/queens-puzzle-chess-problem-solution-software

"Eight Queen" was a puzzle proposed by Chess player Max Betzel in 1848. On the chess board of 8 × 8 square, 8 pieces of Queen / Queen which can go anywhere in the vertical and horizontal directions and oblique direction are arranged, but in that case, it is "a position where every piece is taken by another piece You can not do it "rule is set. How many correct answers exist in conformity with this rule has been regarded as a mystery for a long time, but Gunther suggested a method to solve using determinant in 1874 when more than 100 years passed since devising We have confirmed that the total solution (basic solution) is 12 by Glaisher in England.


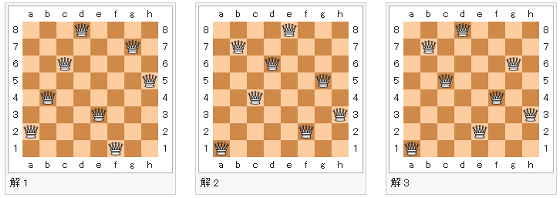
This problem made the number of squares on one side of the chessboard equal to the number of queenn - Queen problemIt is also known that the number of solutions increases dramatically as the number of n increases. At the time of writing, all the solutions are found in "26 - Queen" calculated by Dresden University of Technology in 2009, its basic solution is 2789 trillion, 712.4 billion 665,1 289 pieces, variations such as inverted form If we include solutions, we know that the number will be 2 1,171,699,616,336,444.

A research team by Dr. Ian Gent and others, a computer scientist at St Andrews University,n - Queen filling problem"(N-Queens Completion) on the complexity of puzzles(PDF)paperIs being created. The n - queen filling problem is a puzzle problem that fills the rest of the queen in advance with some queen pieces lined up on the chess board in advance.

Basically in order to solve this problemBacktrack methodIn other words, the "brute force law" is used, so to speak, it takes a huge amount of time to try all the options, and the time increases rapidly exponentially as the number of masses and queen increases I will. According to Gent, as the development of computers and algorithms capable of quickly solving this "n-Queen filling problem" advances, we can expect the evolution of technology that solves our daily problems. As mentioned earlier, the n - Queen problem that can be solved by modern science has remained in "26 - Queen" of 26 × 26 square, so even if it is a hole filling problem, It is essential to develop new technologies that do not yet exist.

This problem was set up in 2000 by the American Clay Mathematics Institute together with a million dollar prize money (about 110 million yen)Millennium prize questionIt is said to lead to the proof of "P versus NP problem" counted as one of the factors. This is a problem when it is regarded as an NP problem, "a problem that can be solved quickly and quickly" is regarded as a problem P, although "it may be difficult to find an answer, but it is possible to quickly check whether there is an answer or not" It is proved that all P problems that can be solved quickly are NP problems that can quickly confirm the answer ", but the opposite, that is, prove the problem of" can all the NP problems quickly confirm the answer be solved quickly " thing. In order to solve this, it is necessary to calculate a huge amount of calculation quickly, and it is thought that tens of thousands of years will be required for the solution even with modern computer technology.