なぜ数を「0」で割ってはいけないのか？

数学の世界では、ルールを変えれば奇妙な答えであっても存在することが可能になります。しかし、「数をゼロで割るな」というルールは、多くの場合「破ってはいけないもの」と言われます。なぜ「ゼロで割るな」というルールを破るべきではないのかを、アニメーションでわかりやすく解説したムービーが公開中です。

Why can't you divide by zero? - TED-Ed - YouTube

「数をゼロで割るな」というルールが説かれるのは、ゼロの性質ゆえ。基本的に、「10÷2＝5」「10÷1＝10」のように、ある数を小さな数で割るほど、解は大きくなります。

この関係性をグラフにするとこんな感じ。縦軸を商、横軸を「10を割る数」で表すと、割る数がゼロに近づくほど商が大きくなっており、10をゼロで割ると商が無限大になるかのように思えます。

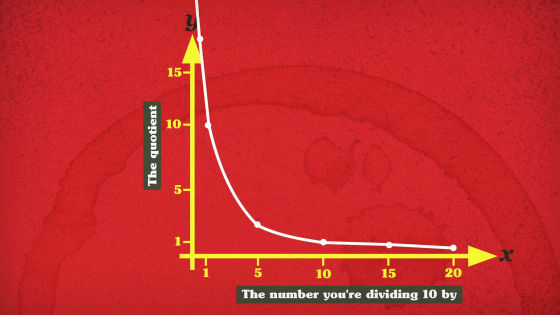
しかし、実際には「10÷0」は無限大ではありません。

このことを理解するためには、「割り算」の本当の意味について知る必要があります。

「10÷2」は、「10を作るには2を何度足せばいいのか？」ということを意味します。

あるいは、「2×何が10になるのか？」という言葉でも言い換えられます。

割り算は必然的にかけ算の裏返しなのです。

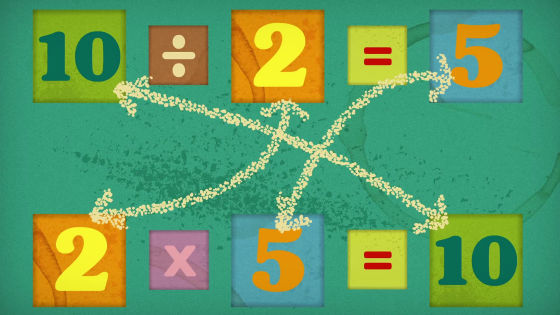
「X」という数でかけたときの答えを、元の数に戻す時には逆数をかける必要があります。

例えば3に2をかけて6を求めた時は、2の逆数である2分の1を6にかければ3が導きだされます。

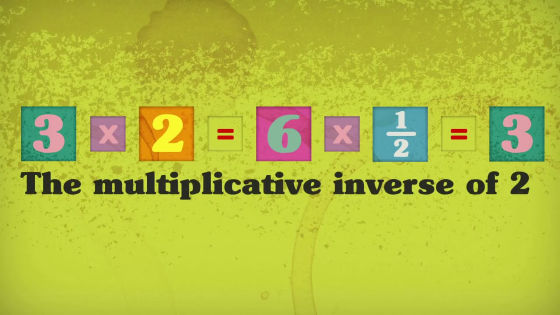
この時、数に逆数をかけると、かならず1になります。

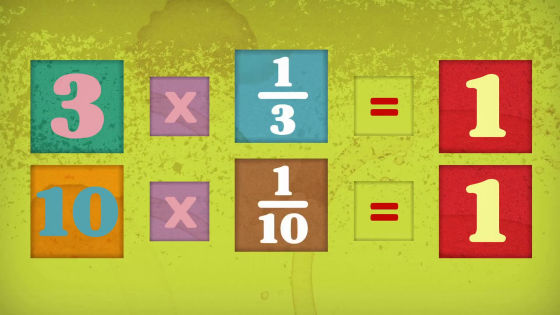
逆数のルールにのっとれば、0の逆数は0分の1になり、0に0分の1をかけると1になる、という関係があるはずなのです。

しかし、周知の通り、0に何をかけても0になるので、「0の逆数」はあり得ません。

数学者はこれまでいくつものルールを破ることで、さまざまな答えを可能にしてきました。例えば、負の数の平方根はもともと存在しませんでしたが、数学者が「虚数(i)」と呼ばれる数を作り出したことで、新たに複素数の世界を開くことができました。

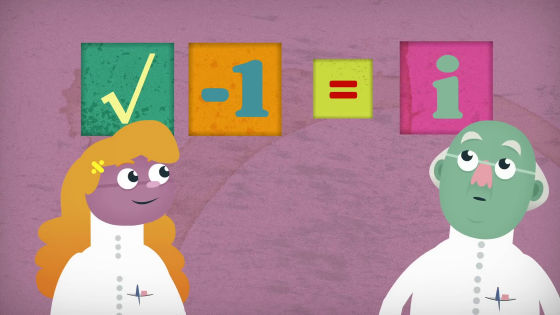
「i」を作り出すことが可能ならば、0の逆数の問題も新たなルールを作ることで解決できるはず。では無限大を0分の1するというルールを作ると、どうなるでしょうか？

逆数の法則に従えば、「∞＝1／0」は「0×∞＝1」に言い換えられるはず。

さらに、(0×∞)＋(0×∞)は2になるはず。

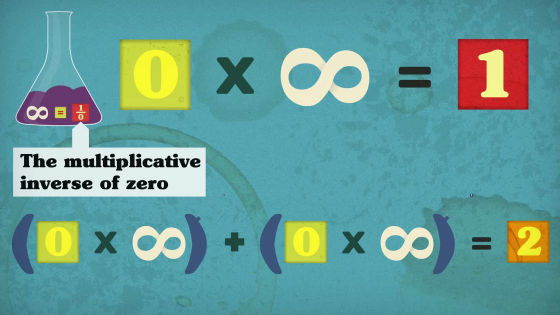
この式を展開すれば(0＋0)×(∞)＝2になり……

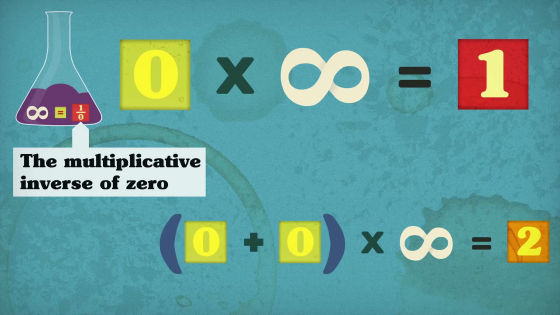
最終的に0×∞＝2という式ができます。しかし、最初に示したように「0×∞＝1」なので、最終的に「1＝2」という答えが導きだされてしまいます。

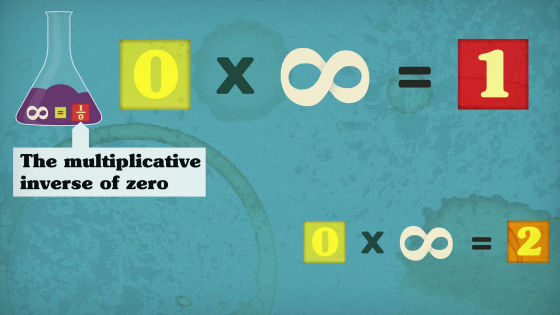
「1＝2」という考えは、私たちが通常用いる数の世界では真実ではないだけで、必ずしも間違っているとは言えません。数学の世界では、1や2、あるいはそれ以外の数が0と等しいといえれば、この考えも数学的に妥当となります。

しかし、「1／0＝1」を有用としたリーマン球面をのぞき、「∞＝1」という考えは、数学者やそれ以外の人にとって有用とは言えません。

有用でないために「0で割るな」というルールは基本的には破られるべきではないのですが、だからといってこれは、我々が数学的なルールを破ろうと実験することを止めるべき、ということを意味しません。私たちはこれから探索する新しい世界を発明できるかどうか、実験していくべきなのです。