Why should not we divide the number by "0"?

In the world of mathematics, changing rules will enable you to exist even if we have strange answers. However, the rule "Do not divide numbers by zero" is often said to be "you should not break". Why Should not break the rule that "Do not divide by zero", is it in the public movie that explains easy-to-understand animations.

Why can not you divide by zero? - TED - Ed - YouTube


It is because of the nature of zero that the rule "Do not divide numbers by zero" is to be explained. Basically, as you divide a number by a small number, such as "10 ÷ 2 = 5" or "10 ÷ 1 = 10", the solution gets bigger.


Graphing this relationship is like this. When the vertical axis is quotient and the horizontal axis is expressed as "divide by 10", the quotient is larger as the divide number approaches zero, and it seems that if you divide 10 by zero, the quotient will be infinite .


However, in reality "10 ÷ 0" is not infinite.


To understand this, it is necessary to know the real meaning of "division".


"10 ÷ 2" means "How many times can I add 2 to make 10?"


Or, it can be paraphrased by the word "2 × what becomes 10?"


Division is inevitably the inside of multiplication.


When returning the answer when the number is multiplied by "X" to the original numberReciprocalIt is necessary to put on.


For example, when 3 is multiplied by 2 to find 6, 3 is derived if 6 is multiplied by one half of the reciprocal of 2.


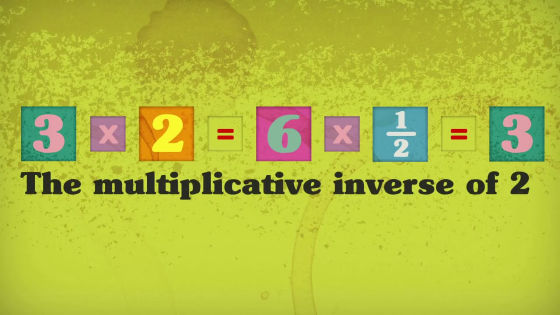
At this time, multiplication by reciprocal number will always be 1.


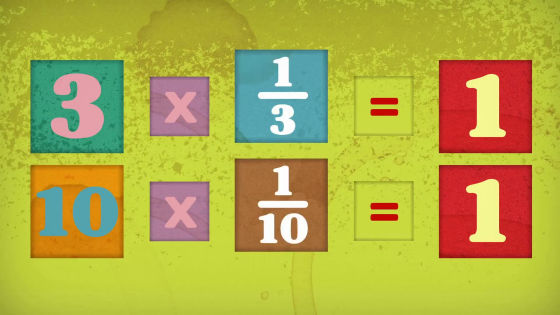
According to the reciprocal rule, there is a relation that the reciprocal of 0 becomes 1/0, and when 0 is multiplied by 0, it becomes 1.


However, as it is well known, "0 reciprocal" is impossible because it becomes 0 regardless of what is applied to 0.


Mathematicians have enabled various answers by breaking many rules so far. For example, the square root of a negative number did not originally exist, but as a mathematician created a number called "imaginary number (i), we could open a new world of complex numbers.


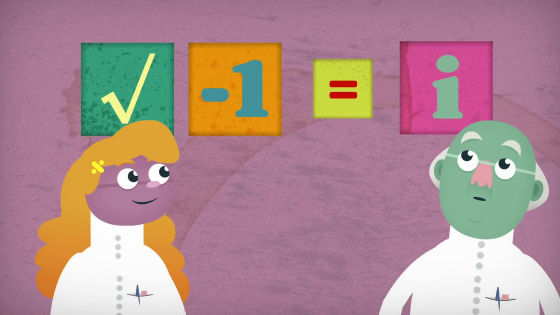
If it is possible to create 'i', the problem of reciprocal of 0 should be solved by creating new rules. So, what happens when you make a rule that infinite is divided by 0/0?


According to the reciprocal law, "∞ = 1/0" can be paraphrased to "0 × ∞ = 1".


Furthermore, (0 × ∞) + (0 × ∞) should be 2.


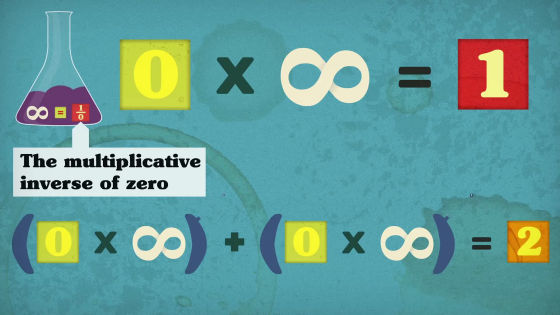
Expanding this equation (0 + 0) × (∞) = 2 ... ...


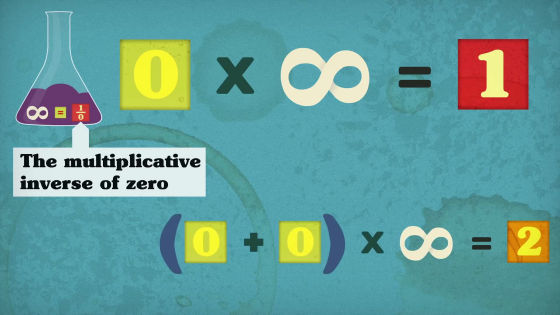
Finally it can be expressed as 0 × ∞ = 2. However, as shown at the beginning, since "0 × ∞ = 1", the answer "1 = 2" will eventually be led.


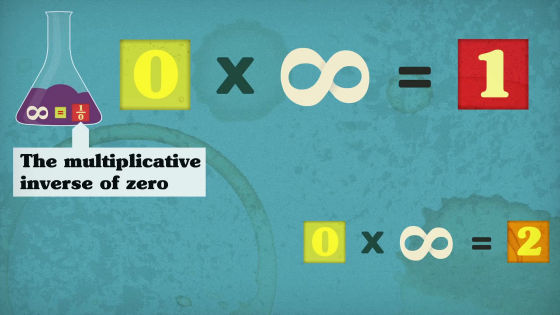
The idea of ​​"1 = 2" is not true in the number of worlds usual, and it can not be said that it is necessarily wrong. In the world of mathematics, this idea is mathematically reasonable, assuming that 1, 2, or any other number is equal to 0.


However, "1/0 = 1" was made usefulRiemann sphere, The idea of ​​"∞ = 1" is not useful for mathematicians and other people.


In order not to be useful, the rule "Do not divide by zero" should not be basically broken, but that does mean that we should stop experimenting to break mathematical rules I will not. We should experiment to see if we can invent the new world to explore in the future.