Feb 17, 2025 20:00:00

Why is it difficult to create a calculator app, and what are the innovations behind Android's 'Calculator'?

Smartphones and PCs are equipped with calculator apps, which allow you to instantly find the answer for simple calculations. However, it is very difficult to develop a calculator that can display accurate answers, and as an example, engineer Chad Nauseam explains how the 'Calculator' app installed on Android was developed.

calculator-app - Chad Nauseam Home

https://chadnauseam.com/coding/random/calculator-app

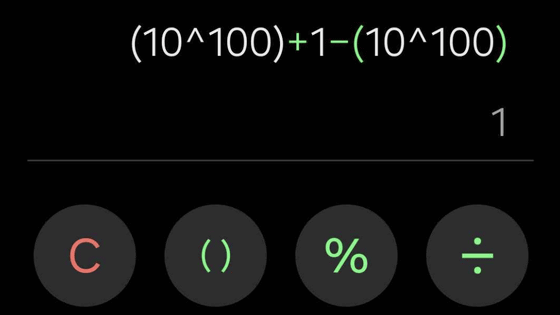
Below is the result of calculating '(10 ¹⁰⁰ ) + 1 - (10 ¹⁰⁰ )' using the iOS 'Calculator'. Normally, the answer would be '1' because 10 ¹⁰⁰ would be canceled out. However, the result of the calculation by the calculator is '0', indicating an error.

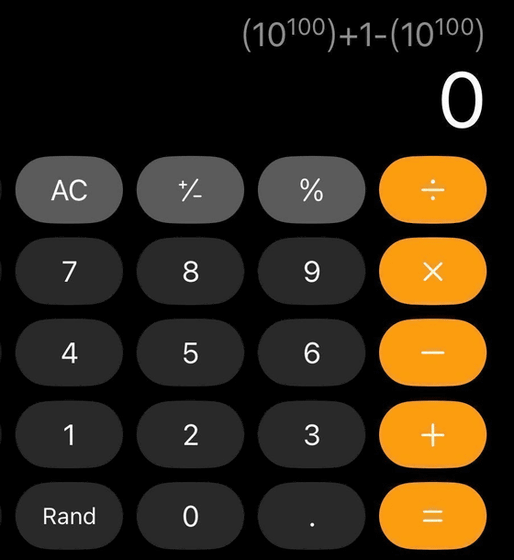
When I ran the same calculation on the Android calculator, the answer came out as '1'.

Although it may seem easy to use a calculator because it just calculates numbers, accurate calculations are difficult because

floating-point arithmetic is performed on the computer. When expressing a decimal number as a 64- bit double-precision floating-point number according to the IEEE 754 standard, it is divided into 'positive/negative sign (1 bit) + mantissa (11 bits) + exponent (52 bits)', so the numbers that can be expressed as 64-bit double-precision floating-point numbers are discrete, and if they cannot be expressed exactly in binary, they are rounded to the nearest representable value. As a result, even simple numbers such as 0.1 may not be expressed exactly.

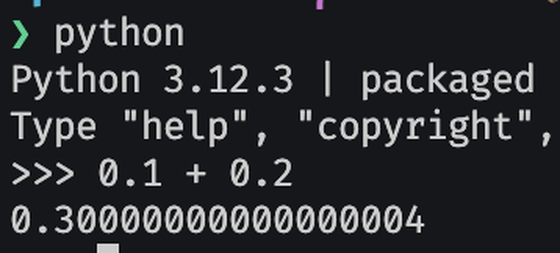
For example, here is the calculation of 0.1 + 0.2 in the Python 3.12.3 console: The answer is 0.3, but the calculation result is shown as '0.300000000000000004'.

The Android Calculator was designed by Hans Boehm, the developer of the Boehm Garbage Collector, a garbage collector for C/C++. When developing the Calculator app, Boehm wondered how to make calculations more accurate.

One way to perform more accurate calculations is to use 'rational number arithmetic' using a data type called 'bignums' for handling arbitrary precision integers . Unlike normal numeric types, bignums can represent integers with no size limit, so it is possible to accurately handle huge numbers such as 10 ^100. For example, bignums makes it easy to calculate fractions by using bignums for both the numerator and denominator. This makes it possible to implement rational numbers accurately.

However, 'rational number arithmetic' cannot express numbers that cannot be expressed as fractions, i.e. irrational numbers such as π and √2. Of these, √2 can be expressed as the solution of a polynomial with a favorable coefficient, 'x ² - 2 = 0,' so 'algebraic arithmetic,' which expresses numbers as polynomial equations, can be used. However, π is a transcendental number , so it cannot be expressed as a polynomial with a favorable coefficient.

The solution to this problem is the idea of 'recursive real number arithmetic,' which sets the significant digits that represent the precision and outputs rational numbers that satisfy that precision.

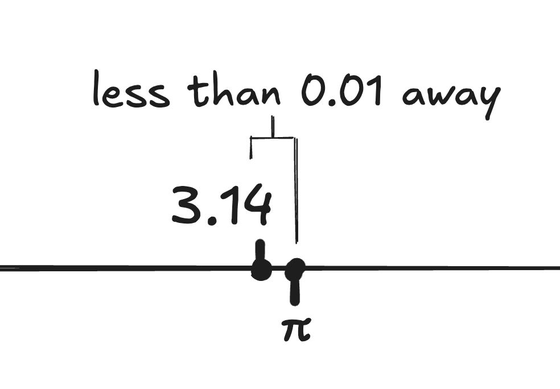
For example, when using recursive real number arithmetic to find pi, it will return 3.14 in response to the request 'Find pi to within 0.01 accuracy,' and it will return 3.141 in response to the request 'Find pi to within 0.001 accuracy.'

Furthermore, if you want to find 2π to within 0.01 error, multiplying π by 2 will double the error, so π must be calculated as 3.141, which is accurate to within 0.005 error, and then multiplying this by 2 returns 2π = 6.282, which is accurate to within 0.01 error.

Recursive real number arithmetic makes it possible to calculate irrational and transcendental numbers, but since it only approximates within a specified error range, errors will inevitably occur. For example, this can lead to problems such as the calculation result '1-1 = 0.00000000000000000' being output, or the display showing sinπ = 0.0000000000000000.

So, in developing the 'Calculator' app, Boehm combined rational arithmetic with recursive real arithmetic. Simple calculations using integers use only rational arithmetic, so an exact answer can be obtained immediately, while calculations involving π or √2 use recursive real arithmetic to perform approximate calculations. This makes it possible to meet both requirements necessary for a practical calculator: '1-1' can be displayed as a perfect 0, and '1+e^(-1000)-1' can be displayed as a small positive number.

Furthermore, when 'arg' is a rational argument, Boehm introduced symbolic expressions that express numbers as functions, such as πarg, √arg, e ^arg , ln(arg), log ₁₀ (arg), sin(πarg), and tan(πarg). This allows π and e to be treated as symbols rather than infinitesimals, and sinπ can be output as 0.

For example, when calculating 1×π + 3×π, 1×π and 3×π can be treated as symbolic expressions, so only the rational part, 1 + 3, is calculated to obtain the symbolic expression, 4π. This makes it possible to achieve practical calculation speeds while maintaining the highest possible accuracy.

Nauseam commented, 'I hope that the next time you use an Android calculator, you will understand its value a little more.' Boehm has published the following paper summarizing his research on the development of the calculator.

Towards an API for the Real Numbers
https://research.google/pubs/towards-an-api-for-the-real-numbers/