勝てる賭けに挑むときは「所持金の何％」を投じるべきなのか？

未来を読むことは不可能ですが、時折「勝てそうな賭け」に出くわすことがあります。しかし、「Don’t put all your eggs in one basket(全ての卵を1つのカゴに入れるな)」ということわざがあるように、一度の賭けに多額の所持金を投じるというのはリスクを伴う行為です。「勝てそうな賭けに投じる資金はどのくらいがベストなのか？」という疑問について、数式処理システム「Mathematica」の開発元であるWolfram Researchが解説しています。

The Kelly Criterion
https://fhur.github.io/notes/articles/the-kelly-criterion/index.html

今回Wolfram Researchが解説しているのは、「Kelly Criterion(ケリー基準)」という賭けを複数回行う際に利益を最大化する賭け方に関する理論です。今回はケリー基準のモデルを解説するため、ごくごく簡単な「コイントス」のギャンブルについて考えます。

コイントスを考える時、通常は「表が出る確率」と「裏が出る確率」はそれぞれ50％に設定します。しかし、今回は「勝てる賭けに挑む」、つまり「表が出る確率pをあらかじめ知った状態」で賭ける場合を考えます。そして、賭けをn回繰り返した時の所持金Snが最大となるような「所持金から賭けるお金の割合f」を求めます。なお、コイントスに勝った場合は賭け金が2倍になって帰ってきますが、負けた場合はそのまま賭け金は没収されます。

例えばf=0.1、すなわち常に所持金の10％を賭ける場合を考えます。

最初の所持金を1000円とした場合、プレイヤーの賭け金は1000円×0.1＝100円で、手元には900円が残ります。もし賭けに勝った場合、100円×2＝200円を獲得できるため、手元に残った900円と合わせると1100円になります。ただし、賭けに負けると100円は没収されるので、所持金は900円のまま。つまり、所持金は賭けに勝つと(1＋0.1)＝1.1倍に、賭けに負けると(1-0.1)＝0.9倍になります。

一般化すると、要するにこのギャンブルは「勝てば所持金が(1＋f)倍になって、負ければ所持金が(1-f)倍になる」ということの繰り返しです。この点を踏まえ、勝った回数Wと負けた回数Lを新たに導入すると、所持金は以下のようになります。

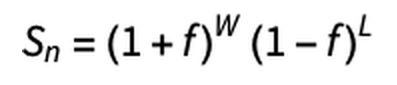
このギャンブルは「出方が偏ったコイン」を使って、毎回表に賭けるという設定です。賭けにn回挑戦した時に勝つ確率pは、「賭けに勝った回数W」÷「賭けに挑戦した回数n」で求められます。一方、負ける確率(1-p)は「賭けに負けた回数L」÷「賭けに挑戦した回数n」で求まります。つまり、W＝n×p、L＝n×(1-p)と表わすことができます。

この2式を先ほどの式に代入すると以下のようになります。

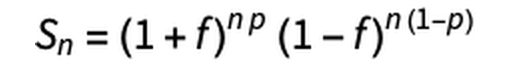
求めるものは、「賭けに挑む際、所持金の何％を投じるのがベストなのか？」に対する答えです。これは言い換えれば「Snを最大化するfを求めたい」ことになります。なお、nは回数、pは出目の偏り(不変)なので、fはプレイヤー側が唯一制御できる変数でもあります。

今回のギャンブルは「出方が偏ったコイン」を使っており、プレイヤー側はこの偏りを利用して有利な賭けを繰り返しているという設定です。有利な賭けが確定しているという状況は、直感的には「賭けに投じる割合を増やしたい、いっそオールイン(全賭け)すべきでは」と思えます。しかし、試行を複数回繰り返すという点に意識を向けると、「投じる割合を高く設定してしまうと、負けが込んだときに資金がごっそり減ってしまう。オールインに至っては、一度でも負けたならばそこで終わる」ということに気づきます。というわけで、今回のテーマは「破綻のリスクを完全に回避しながら、できる限り早く所持金を増やすためのfを求めること」です。

このテーマを考えるため、試行を無限大繰り返した際の最終的な資金額と初期資金の比率を比べた「指数関数的成長率」と呼ばれる以下のGを導入します。このGは、設定されたfとpに対し、賭けを繰り返した結果として最終資金が増えるならば正の値、最終資金が減るならば負の値を取ります。

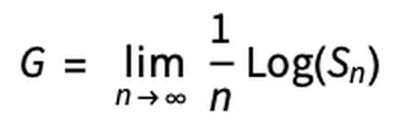
このとき、fとGを変数とするグラフは以下のようになります。

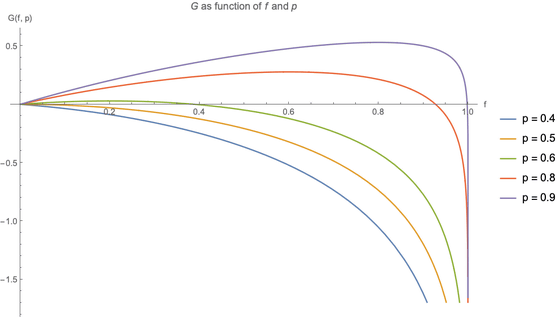
p＝0.4(賭けに勝つ確率が40％)のときはいかなるfを設定しようとGは負の値を取り、結局のところ「負ける賭けに挑む場合は、fをどのように設定しても最終的な資金は減る」という当たり前の事実がわかります。一方、p=0.5(賭けに勝つ確率が50％)のときもいかなるfを設定しようとGは負の値を取り、「試行を無限回行った場合は確率50％の賭けでも絶対に損する」ということがわかります。これは、一定の確率で資金がゼロになって破綻するという可能性が存在することが原因です。

p＝0.6(賭けに勝つ確率が60％)以上では、fが適切な範囲ならばGが正の値を取るものの、fが大きすぎると負の値になります。pから最適なfを算出する方法については高度な数学が必要とのことで省略されていますが、「f＝2p-1」のときにGが最大化し、ベストな結果が得られるとのこと。つまり、60％の確率で勝てるギャンブルに挑む場合は、f＝0.6×2-1＝0.2、つまり所持金の20％を賭けるのがベストということです。