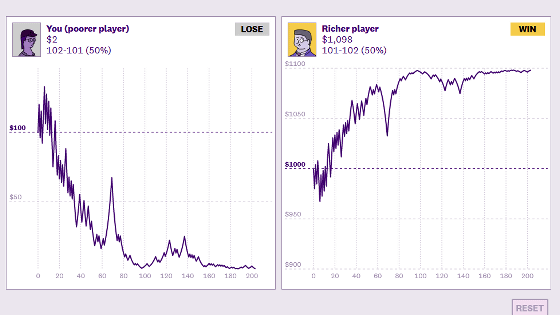
What percentage of your money should you invest when you challenge a winning bet?

It's impossible to read the future, but sometimes you come across 'winning bets'. However, as the saying goes, 'Don't put all your eggs in one basket, ' putting a large amount of money in one bet is a risky act. is. Wolfram Research, the developer of the computer algebra system Mathematica, explains the question, 'What is the best amount of money to invest in a bet that is likely to win?'

The Kelly Criterion
https://fhur.github.io/notes/articles/the-kelly-criterion/index.html

This time, Wolfram Research is discussing the theory of betting that maximizes profits when making multiple bets called 'Kelly Criterion'. This time, to explain the Kelly-based model, let's consider a very simple 'coin toss' gambling.

When considering a coin toss, the 'probability of flipping' and 'probability of flipping' are usually set to 50% each. However, this time, let's consider the case of betting 'challenge a winning bet', that is, ' a state in which the probability p of the appearance of the table is known in advance'. Then, possession gold Sn when the bet was repeated n times will determine the 'percentage f of money gambling from the possession of money' as a maximum. If you win the coin toss, your stake will be doubled and you will return, but if you lose, your stake will be forfeited.

For example, consider f = 0.1, that is, always bet 10% of your money.

If the initial possession is 1000 yen, the player's stake is 1000 yen x 0.1 = 100 yen, and 900 yen remains at hand. If you win the bet, you will get 100 yen x 2 = 200 yen, so if you add the 900 yen you have left, it will be 1100 yen. However, if you lose the bet, 100 yen will be forfeited, so your money will remain at 900 yen. In other words, if you win the bet, your money will be (1 + 0.1) = 1.1 times, and if you lose your bet, it will be (1-0.1) = 0.9 times.

In general, this gambling is a repetition of ' If you win, your money will be (1 + f) times, and if you lose, your money will be (1-f) times.' Based on this point, if you newly introduce the number of wins W and the number of losses L , the amount of money you have will be as follows.

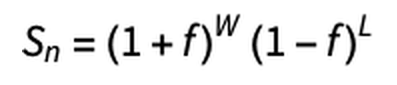
This gambling is set to bet on the table every time using 'coins with a biased appearance'. The probability p of winning when a bet is challenged n times is calculated by 'the number of times a bet is won W ' ÷ 'the number of times a bet is tried n'. On the other hand, the probability of losing (1- p ) is calculated by 'the number of times you lost a bet L ' ÷ 'the number of times you tried a bet n '. That is, it can be expressed as W = n × p and L = n × (1- p).

Substituting these two equations into the previous equation gives the following.

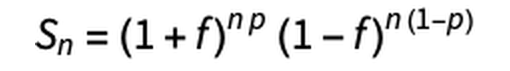
What you are looking for is the answer to 'What percentage of your money is best to invest when you bet?' In other words, 'I want to find f that maximizes Sn.' Note that n is the number of times and p is the bias (invariant) of the outcome, so f is also the only variable that the player can control.

This gambling uses 'coins with a biased appearance', and the player side is set to use this bias to repeat advantageous bets. Intuitively, the situation where a favorable bet has been confirmed seems to be 'I want to increase the proportion of bets I should make, and I should make an all-in (all bets)'. However, when paying attention to the fact that the trial is repeated multiple times, 'If you set a high percentage of investment, the funds will be reduced when you lose. If you lose even once, you will lose. If you do, it will end there. ' So, the theme this time is 'to seek f to increase the amount of money you have as soon as possible while completely avoiding the risk of bankruptcy'.

To consider this theme, we will introduce the following G , called 'exponential growth rate', which compares the ratio of the final amount of funds to the initial amount of funds when the trial is repeated infinitely. This G takes a positive value for the set f and p if the final fund increases as a result of repeated bets, and a negative value if the final fund decreases.

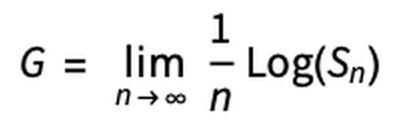
At this time, the graph with f and G as variables is as follows.

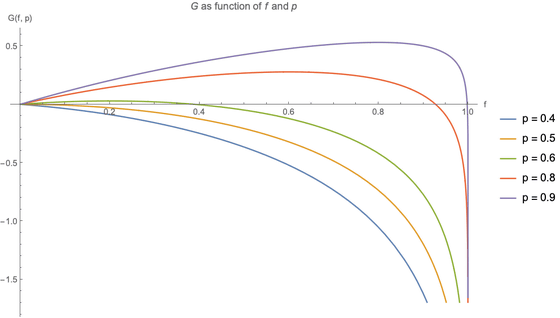
p = 0.4 G attempts to set any f when the (probability of winning the bet 40%) takes a negative value, if it turns out to challenge the 'lose bets, final be set arbitrarily to the f You can see the obvious fact that 'general funds will decrease'. On the other hand, even when p = 0.5 (the probability of winning a bet is 50%), G takes a negative value no matter what f is set, and 'if you make an infinite number of trials, you will definitely lose even a bet with a probability of 50%'. You can see that. This is due to the possibility that there is a certain probability that the funds will go to zero and go bankrupt.

Above p = 0.6 (60% chance of winning a bet), G takes a positive value if f is in the appropriate range , but negative if f is too large. The method of calculating the optimum f from p is omitted because it requires advanced mathematics, but when ' f = 2p-1 ', G is maximized and the best result is obtained. .. In other words, if you are trying to win a gambling with a 60% chance, it is best to bet f = 0.6 × 2-1 = 0.2, that is, 20% of your money.