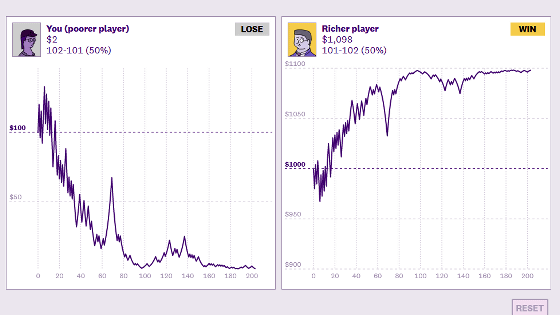
At first glance, it looks absolutely profitable, but if you continue to challenge it, you will be defeated.

' Peter's Coin Toss ' looks like a bet that will always be positive if you ask for the 'average of a large number of participants', but it is a magical coin game that you will suffer a crushing defeat if you actually try it many times. Ole Peters, who devised Peters' coin toss, has released a simulator that shows the horror of the game in one shot.
The infamous coin toss – Ergodicity economics
Peters' coin toss rules are as follows:
・Possession starts from $100
・ If you toss a coin and get heads, you can get 50% of your money.
・If you toss a coin and get tails, 40% of your money will be confiscated.
・You can repeat the coin toss as many times as you like
If you read the rules at once, you will think, 'Since the rate of receiving is greater than the rate of confiscating, if you continue many times, you will definitely make money.' By operating the simulator below, you can calculate the transition of your money when you actually challenge Peters' coin toss.
A simulator that changes the number of participants after 10 rounds
https://coin-n.streamlit.app/
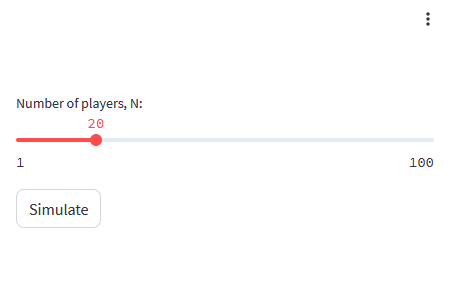
Using the simulator is easy, just move the slider left and right to specify the number of participants in the game and click 'Simulate'.

The result of simulating with one player is as follows. The horizontal axis is the number of rounds in the game, and the vertical axis shows how many times the money has increased from the initial $ 100. If you check the change in your money (blue line), you can see that it has increased to nearly 10 times in the 10th round.
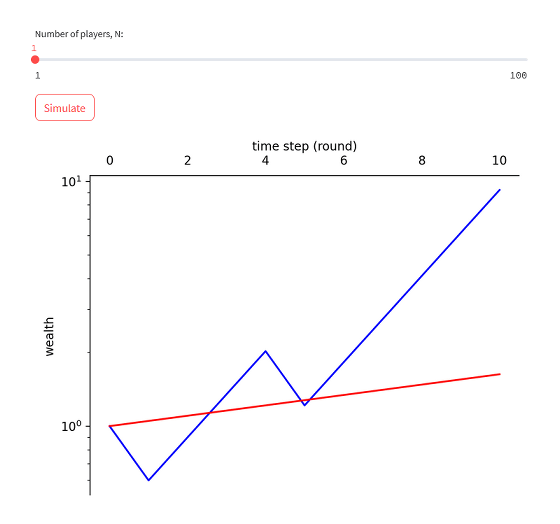
When I simulated again, this time the money I had was reduced to about 1/10.

The average amount of money held by 100 participants changes like this. When the number of participants is specified as 100, the amount of money will increase slightly no matter how many times you click 'Simulate'.
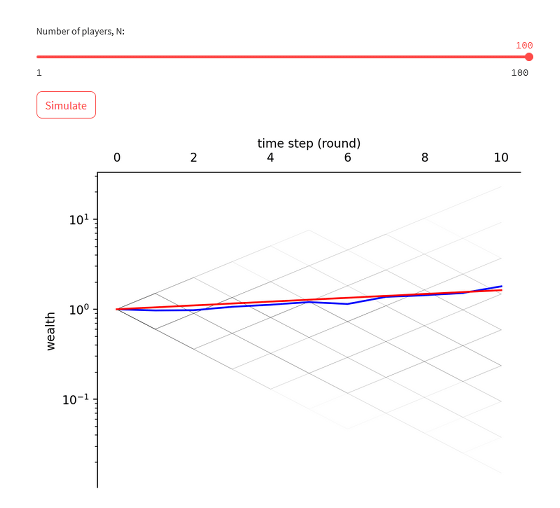
Many people must have thought, ``If the average of 100 people is positive, if you continue to participate, you will definitely have more money.'' The following 'simulator that changes the number of rounds with one participant' blows away such an idea.
A simulator that changes the number of rounds with one participant
After specifying the number of rounds on the left and right sides of the slider, click 'Simulate' to draw a transition graph of your money.

If you play 10 rounds, your final money will be positive or negative.


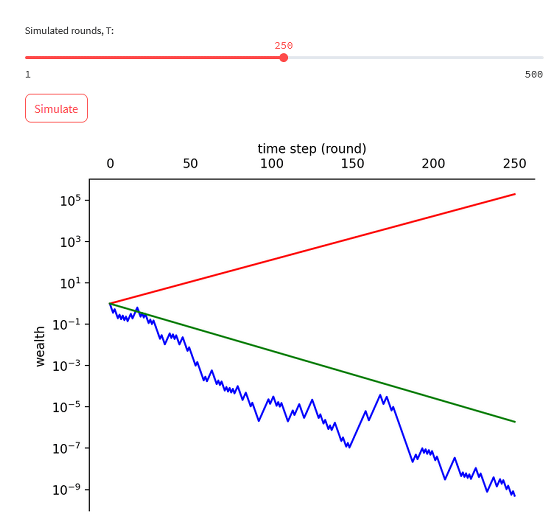
However, as you increase the number of times you line, the frequency with which your money becomes positive decreases. For example, the simulation result when the number of rounds is set to 250 is as follows.
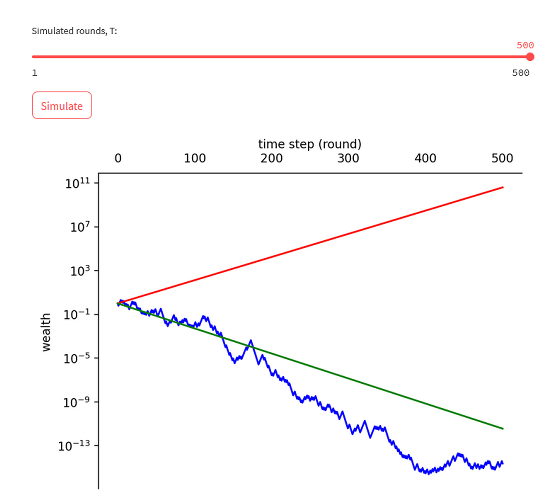
And the simulation results when playing 500 rounds are as follows. My money has become less than 1/10 trillion.
The reason why the amount of money in your possession decreases as the number of attempts increases is simple. For example, if you start with $100 and lose in the first round, your money will be $60 (100-100 x 0.4). And if you win the second round, your money will be 60 + 60 x 0.5 = $90. In other words, one loss cannot be canceled out with one win, so if you continue to play coin games with a 50/50 chance of winning over and over again, you will lose.
In addition, Peters' coin toss is a game created to break down the `` ergodic property '' that the `` time average of one individual '' and the `` average of the group when fixing the time '' are the same. You can check the following movie for a lecture by Mr. Peters himself, ``Break down ergodicity with Peters' coin toss.''
TEDxGoodenoughCollege-Ole Peters-Time and Chance-YouTube
Related Posts: