3Dゲームエンジンで使われている関数を数学的に説明するとこうなる

ベクトル演算のひとつである内積は、二つのベクトルの関係を一つの数字に変換してくれる便利な存在です。そんな内積によるベクトルのエンコードが3Dゲームにおいてどのように役立っているかをエンジニアのMing-Lun "Allen" Chouさんが説明しています。

Gamedev Tutorial: Dot Product, Rulers, And Bouncing Balls | Ming-Lun "Allen" Chou | 周明倫
https://www.allenchou.net/2020/01/dot-product-projection-reflection/

まずは「ベクトルの内積」です。2次元空間上にある始点が同じ2つのベクトルaとベクトルbの内積について考えてみます。感覚的に内積を説明すると、ベクトルbに垂直な方向から光を当てたとき、ベクトルb上にできるベクトルaの影の長さとベクトルbの長さとの積が、ベクトルaとベクトルbの内積になります。

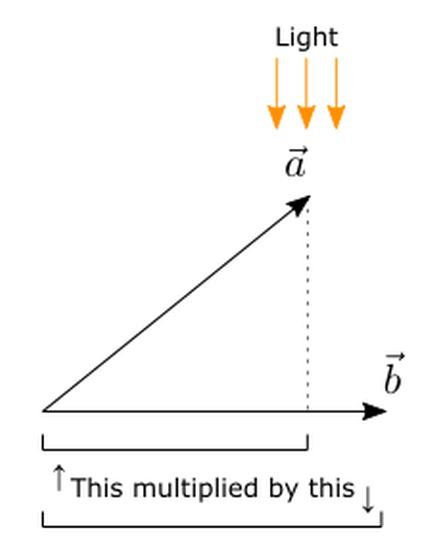
内積は二通りの式で表現でき、三角関数と座標軸を使う方法があります。三角関数を使うと下記の数式のように書くことができます。

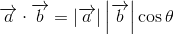
ベクトルaの終点を(a1, a2)、ベクトルbの終点を(b1, b2)とし、座標を使って式に表すとこんな感じ。

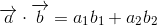
もちろん3次元の空間にも応用可能。その場合は下記のような数式で表されます。

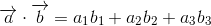
ベクトルの内積の定義が理解できたら、次はベクトルb上にベクトルaを射影したベクトルを導く方法を考えてみます。

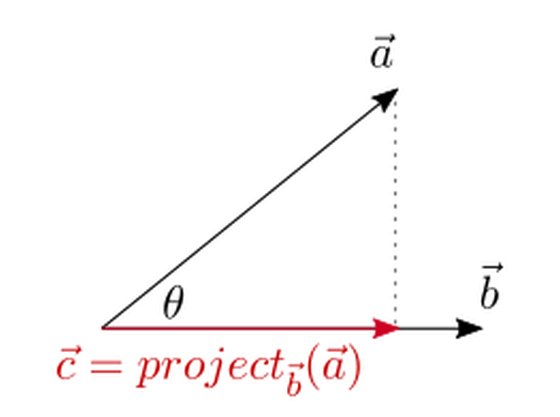
長さが1のベクトルは単位ベクトルと呼ばれ、ベクトルbの単位ベクトルはベクトルbをベクトルbの長さで割ることで求められます。ベクトルcはベクトルb上にあり、大きさはベクトルbに垂直な方向から光を当てたとき、ベクトルb上にできるベクトルaの影の長さ、つまりベクトルaとベクトルbの内積をベクトルbの長さで割ったものなので、ベクトルcは下記の数式のように表すことができます。

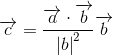
同じベクトル同士の内積はベクトルの長さの2乗に等しいので、下記のように数式を書き直すことができます。

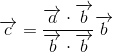
ベクトルbが単位ベクトルの場合は、さらに数式がシンプルに。

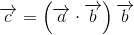
3DゲームエンジンのUnityでは、これまでの数式がすべて関数として整備されています。例えば内積を求める関数はこんな感じ。ベクトルaとベクトルbを入力すると内積が返り値として返されます。

Vector3 Dot(Vector3 a, Vector b)
{
  return a.x * b.x + a.y * b.y + a.z * b.z;
}

射影したベクトルを求める関数はこんな感じで実装されています。vecが射影元のベクトル、ontoが射影先のベクトルとなっていて、先ほどの説明と同じように実装されているのがわかります。

Vector3 Project(Vector3 vec, Vector3 onto)
{
  float numerator = Vector3.Dot(vec, onto);
  float denominator = Vector3.Dot(onto, onto);
  return (numerator / denominator) * onto;
}

これまでの関数を駆使して、Unity上で物体の長さを測る物差しを実装してみます。

まずは起点と物差しの軸を定義します。Baseが起点ベクトルで、Axisが物差しの軸となる単位ベクトルです。

struct Ruler
{
  Vector3 Base;
  Vector3 Axis;
}

次に、起点ベクトルから測りたい対象の点までの相対ベクトルを計算。相対ベクトルは、起点の座標から測定対象の点までを結ぶベクトルです。

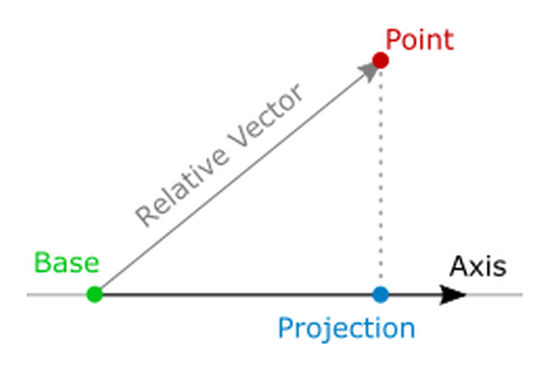
計算式はこんな感じ。

Vector3 relative = vec - ruler.Base;

相対ベクトルと軸となるベクトルの内積を計算し、単位ベクトルを掛けます。今回は軸となるベクトルが単位ベクトルなので、内積と軸となるベクトルの積が射影ベクトルになります。

float relativeDot = Vector3.Dot(vec, ruler.Axis);
Vector3 projectedRelative = relativeDot * ruler.Axis;

最後に起点ベクトルと射影ベクトルとの差分を求めれば長さが求められます。

Vector3 result = ruler.Base+ projectedRelative;

これまでの流れを一つの関数にするとこんな感じになります。

Vector3 Project(Vector3 vec, Ruler ruler)
{
  // 相対ベクトルを計算
  Vector3 relative = vec - ruler.Base;
   
  // ベクトルを射影
  float relativeDot = Vector3.Dot(vec, ruler.Axis);
  Vector3 projectedRelative = relativeDot * ruler.Axis;
 
  // 起点からの差分を計算
  Vector3 result = ruler.Base+ projectedRelative;
 
  return result;
}

Chouさんのウェブサイトでは、光の反射や球体の動きについても詳しく説明されています。説明に使用されている3Dオブジェクトを実際に動かすことができるソースファイルは、開発者であるChou氏のパトロンになると入手できるとのことです。