Jan 26, 2020 22:00:00

Mathematical explanation of the function used in 3D game engine is as follows

Dot product , one of the vector operations, is a useful entity that converts the relationship between two vectors into one number. Engineer Ming-Lun 'Allen' Chou explains how vector encoding by such inner product is useful in 3D games.

Gamedev Tutorial: Dot Product, Rulers, And Bouncing Balls | Ming-Lun 'Allen' Chou |
https://www.allenchou.net/2020/01/dot-product-projection-reflection/

The first is 'dot product of vectors'. Consider the inner product of two vectors a and b with the same starting point in two-dimensional space. To explain the inner product intuitively, when light is applied from the direction perpendicular to the vector b, the product of the length of the shadow of the vector a formed on the vector b and the length of the vector b becomes the inner product of the vector a and the vector b. Become.

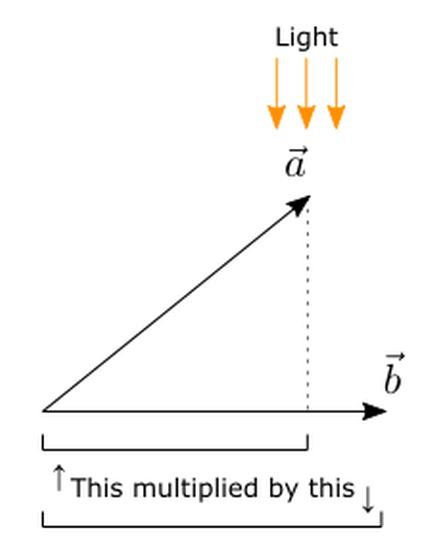
The inner product can be expressed in two ways, using trigonometric functions and coordinate axes. If you use trigonometric functions, you can write like the following formula.

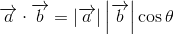
The end point of vector a is (a1, a2) and the end point of vector b is (b1, b2).

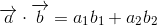
Of course, it can be applied to 3D space. In that case, it is expressed by the following formula.

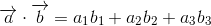
Once you understand the definition of the inner product of the vector, the next step is the vector a on the vector b projection Consider the method of directing the vector was.

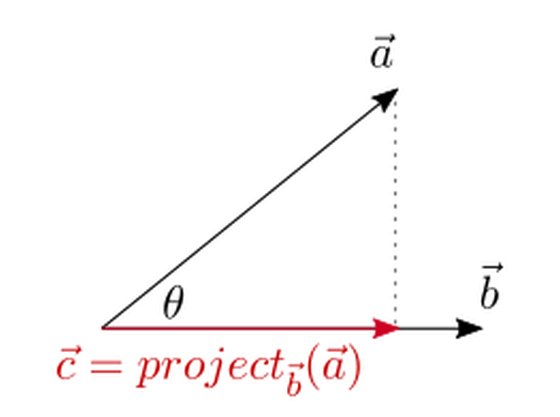
A vector of length 1 is called a unit vector, and the unit vector of vector b is obtained by dividing vector b by the length of vector b. The vector c is on the vector b, and the size is the length of the shadow of the vector a formed on the vector b when light is applied from the direction perpendicular to the vector b, that is, the inner product of the vector a and the vector b is Since it is divided by the length, the vector c can be expressed as the following equation.

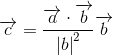
Since the dot product of the same vectors is equal to the square of the length of the vectors, you can rewrite the formula as follows:

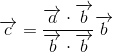
If the vector b is a unit vector, the formula will be even simpler.

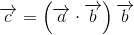
In the 3D game engine

Unity , all formulas so far are maintained as functions. For example, the function to find the inner product looks like this. Inputting vector a and vector b will return the inner product as the return value.

[code] Vector3 Dot (Vector3 a, Vector b)
{
return ax * bx + ay * by + az * bz;
} [/ code]

The function to find the projected vector is implemented like this. You can see that vec is the source vector and onto is the destination vector, which is implemented as described above.

[code] Vector3 Project (Vector3 vec, Vector3 onto)
{
float numerator = Vector3.Dot (vec, onto);
float denominator = Vector3.Dot (onto, onto);
return (numerator / denominator) * onto;
} [/ code]

Using the functions so far, let's implement a ruler to measure the length of the object on Unity.

First, define the starting point and the axis of the ruler. Base is the origin vector and Axis is the unit vector that is the axis of the ruler.

[code] struct Ruler
{
Vector3 Base;
Vector3 Axis;
} [/ code]

Next, calculate the relative vector from the starting point vector to the point to be measured. A relative vector is a vector connecting the coordinates of the starting point to the point to be measured.

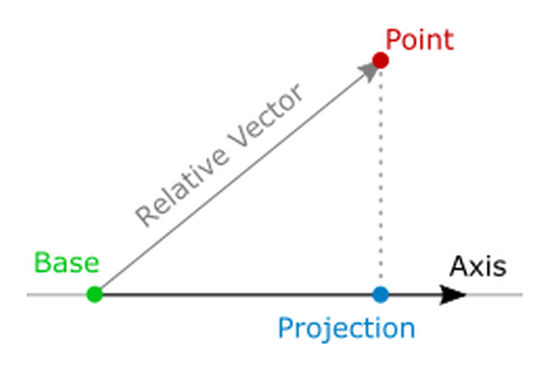
The calculation formula looks like this.

[code] Vector3 relative = vec-ruler.Base; [/ code]

Calculate the dot product of the relative vector and the axis vector and multiply by the unit vector. This time, the axis vector is the unit vector, so the product of the inner product and the axis vector is the projection vector.

[code] float relativeDot = Vector3.Dot (vec, ruler.Axis);
Vector3 projectedRelative = relativeDot * ruler.Axis; [/ code]

Finally, the length can be obtained by calculating the difference between the origin vector and the projection vector.

[code] Vector3 result = ruler.Base + projectedRelative;
[/ code]

If the flow so far is made into one function, it will look like this.

[code] Vector3 Project (Vector3 vec, Ruler ruler)
{
// calculate relative vector
Vector3 relative = vec-ruler.Base;

// project vector
float relativeDot = Vector3.Dot (vec, ruler.Axis);
Vector3 projectedRelative = relativeDot * ruler.Axis;

// Calculate the difference from the starting point
Vector3 result = ruler.Base + projectedRelative;

return result;
} [/ code]

Chou's website also details light reflections and sphere movement. The source file that can actually move the 3D object used in the explanation is available at the patron of the developer Chou.