「無限」という概念を子どもにわかりやすく教えるためにはどう説明すれば良いのか？

By Amos Bühler

無限とは読んで字のごとく「限りが無い」ことを意味する概念ですが、字で読むよりもその内容を頭で理解することは難しいものです。そんな「無限」を子どもにもわかりやすく説明するためにはどうすれば良いのか、コンピュータープログラマーのマーク・ジェイソン・ドミナス氏が解説しています。

The Universe of Discourse : How to explain infinity to kids
https://blog.plover.com/math/infinity-for-kids.html

前置きとしてドミナス氏は、「教育とは、うそをつくプロセスである」という恩師の言葉を挙げています。この言葉が意味するものは決して間違った内容を教えるというものではなく、「〇〇はこういうものである、しかし実際にはこういうものであり、さらにいえば、また別のこういうものである」という風に、まずは細部を省いた総論を伝え、理解に応じて細かい点を掘り下げて教えていくというものであるとのこと。何かを教える時には、まず細かいところからチマチマと教えるのではなく、全体の概念をざくっと理解させた上で、「前はあんな風に説明したけど、もっと正しく言うとこういうことになる」という風に、理解を導いていくことが教育にとって重要であるという考え方です。

そして、この考え方は「無限」というものを理解させる上でも役に立つというのがドミナス氏の考えです。特に、数学に興味を持ってさまざまな疑問を持ち、新たな概念を理解しようとする子どもにとって、この方法は最適であるとドミナス氏は考えているとのこと。無限を辞書で調べると、「限りがないこと。どこまでも続くこと。また、そのさま」などというふうに説明されていますが、実際に全てのものが有限であるこの世界において無限を実感することは実は非常に難しいことであるといえます。

By Mikael Leppä

そんな無限を子どもにわかりやすく伝えるためにドミナス氏が使っている説明が「無限とは、あなたが数えられない最も小さな数」というもの。この説明も少し聞いただけではピンとこないと感じられがちですが、ドミナス氏はこの説明こそが「無限」の概念をあまねく、漏れなく伝えるものであるといいます。

その理由としてまずドミナス氏は「数える」という概念を組み込んでいる事がポイントであると述べています。算数や数学にとって数えるということは全ての基本であり、子どもたちは自然数を数えるという考え方によく慣れています。この「数える」という概念を超えるものとして無限が存在する、と説明することでその概念を理解させるというものです。さらにドミナス氏はここで「まず、数えられる限界の数字を頭に浮かべて下さい。そしてそこにさらに一つを足してみます。それが無限です」というふうに説明するそうです。

ここで勘の良い子どもたちは「それじゃ、無限の次には何が来るの？」と尋ねてくるとのこと。無限が「最終」や「究極」を意味するωであると考えると、ここでよく持ち出される答えは「無限の後には何も来ない」というものですが、ドミナス氏によるとこれは必ずしも正しくないとのこと。ドミナス氏はその答えを「無限＋1」と表しています。

そう答えるとさらに浴びせられる質問が「それじゃ、無限＋1の次には何が来るの？」というものになるといいます。しかし、ドミナス氏によると頭の良い子どもはここで「2⋅ω」の存在に気がつき、さらには「ω−1」について尋ねてくる子どもも現れるとのこと。そうなると、この子どもたちは「ω」は大小のある後続順序数ではなく、0でも後続順序数でもない極限順序数であることを理解することにつながります。

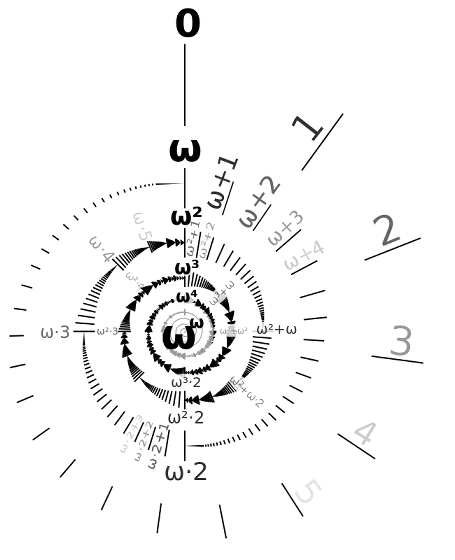
また、別の子どもからは「もし『無限＋1』と『無限』が等しいものでないとすれば、どのような場合において順序数の加算の非可換性について考えることができるのか」という質問が来る事も考えられるとのこと。これについては、「＋1」を数列の先頭に持ってくるとそれは「無限」と同じことになりますが……

数列の後端に「＋1」を持ってくるとまた異なったものになるとのこと。

ドミナス氏によると、これらの図解は無限の基本性質をよく表すデデキントの公理を具現化したものであるとのこと。用語としては難解に感じられますが、このように図で示すといくらか理解しやすくなるものです。

ドミナス氏は最終的なまとめとして、「まずは『ω』を使うこと」とアドバイス。そうすることで、興味や疑問を持った子どもたちが次々に説明を求めてくるので、その時は冒頭で触れたように、「最初の説明は全てを説明していなかったけど、実は細かい部分の話しをするとこんなふうになって……」と、大きな概念から細かい細部へと理解を導くことができるようになると述べています。