How can I explain how to teach children the concept of 'infinity' in an easy-to-understand way?

By Amos Bühler

Infinite is a concept that means "there is no limit" as it reads, but it is difficult to understand its contents with the head rather than reading in a letter. Computer programmer Mark Jason Dominus explains how to explain such 'infinity' in an easy-to-understand way for children.

The Universe of Discourse: How to explain infinity to kids
https://blog.plover.com/math/infinity-for-kids.html

As a preface, Mr. Dominas cites the teacher's word "education is a process of lying". What this word means is not to teach the wrong content nor to say that "○ ○ is such a thing but actually it is such thing, in other words, it is another kind of thing" It is said that it tells the general theory which omitted the details first, and tells down the detailed points in accordance with understanding. When teaching something, first of all I did not teach it with fine details from the details, rather than letting me understand the whole concept, "I explained it like that before, but if I say more correctly it will be like this" It is the idea that guiding the understanding to the wind is important to education.

And Mr. Dominus thinks that this way of thinking is useful to make people understand "infinity". In particular, Mr. Dominus thinks that this method is optimal for children who are interested in mathematics and have various questions and understand new concepts. If you examine the infinite in the dictionary, you can explain infinite in this world where all things are finite, although there are explanations such as "There is no limit, continuing everywhere ... and that" etc. Actually it can be said that it is very difficult.

By Mikael Leppä

To explain such limitlessly to the child, the explanation that Mr. Dominus uses is " infinity is the smallest number you can not count ". Although it tends to be felt that it does not come with a pin just by asking a little about this explanation, Mr. Dominus says that this explanation is what it conveys without omission, all the concept of "infinity" in any way.

First of all, Mr. Dominus says that incorporating the concept of "counting" is a key point. To count for arithmetic and mathematics is all the basis and children are used to the idea of ​​counting natural numbers well. To explain that there is infinite as exceeding the concept of "counting" is to make the concept understood. In addition, Mr. Dominus says, "First of all, let's count the numbers of the limits that can be counted, add one more to it, it's infinite."

The intelligent children here are asking "Well then, what is coming next to infinity?" When thinking that infinity means ω which means "final" or "ultimate", the answer that is often brought here is "nothing comes after infinity", but according to Mr. Dominus this is not necessarily incorrect And that. Mr. Dominus expresses the answer as "Infinite + 1".

If you answer so, the question that gets more exposed will say "Then, what will come next to infinity + 1?" However, according to Mr. Dominus, a smart child notices the existence of "2 ω" here, and furthermore, a child who asks about "ω - 1" will also appear. Then, this child leads to understanding that "ω" is not a successive order number of large and small, but an extreme ordinal number that is neither 0 nor the following ordinal number.

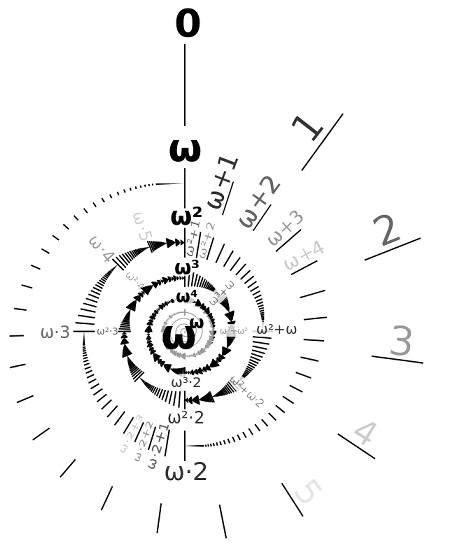
Also, from another child "If infinity + 1" and "infinity" are not equal, the question comes about when in what cases can you think about non-commutativity of addition of ordinal numbers? " Things can also be thought. As for this, if you bring "+ 1" to the beginning of the sequence, it will be the same as "infinity" ... ...

It is said that it will be different if you bring "+1" to the back end of the sequence.

According to Mr. Dominus, these illustrations embody Dedekind's axiom that represents an infinite basic character well. Although it seems to be difficult to understand as a term, it becomes somewhat easier to understand as shown in this figure.

As a final summary, Mr. Dominus advises, "First of all use" ω ". By doing so, children with interests and doubts will ask for explanations one after another, so at that time, as mentioned at the beginning, "Although the first explanation did not explain everything, in fact, When talking, it will become like this ... ... "states that it will be able to lead to understanding from a big concept to detailed details.