Why do prime numbers draw spirals?
At first glance, seemingly random primes can appear to form a spiral when combined from any point of view. Mathematician Grant Sanderson explains how these properties are linked to the appeal of mathematics.
3Blue1Brown - Why do prime numbers make these spirals?
Consider placing a point on a two-dimensional plane. In the image below, the point (1,1) is at an angle of 1 radian and a distance of 1 from the origin. Similarly, place the points (2,2)(3,3)(4,4).
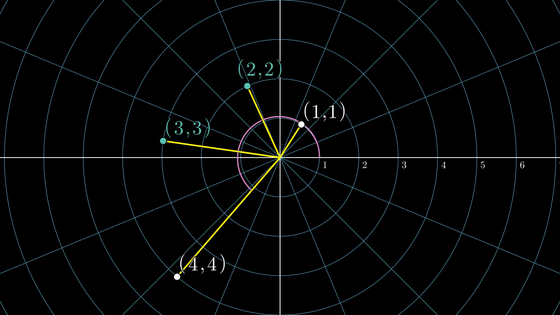
If you continue to increase the number of points in this way, it will gradually spread out in a spiral shape, forming a figure called 'Archimedes' spiral'.
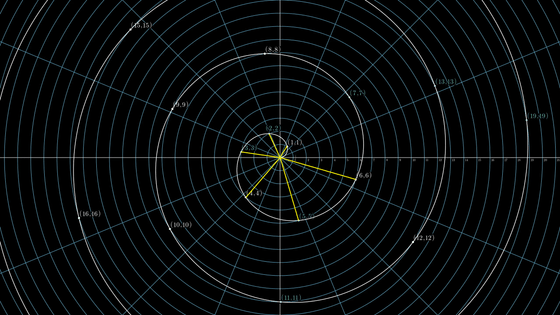
If you remove anything other than prime numbers from this figure, it looks like this. It is said that the part with a hole is a prime number, but I don't think it's very regular.
However, looking at this on a larger scale reveals another pattern. The holes are still there, but it looks like the light bundles are split into four. If you play the video below, you can see how it highlights four clumps.
If you look more closely, the fine spiral consists of 20 lines, and on a larger scale it looks like a total of 280 lines are clustered together.
However, such regularity is not limited to prime numbers, and similar lines appear even if only integers are picked up. However, it is a mystery why such regularity is born, and if we focus only on prime numbers, we will reach one of the most important theorems on the distribution of prime numbers, ' Dirichlet's theorem '.
If you look deeper into the spiral, you can see that a regular sequence of numbers makes up a single line. One is a multiple of 6 (6k), the next line is 6k+2, the next is 6k+3, and so on, and the number 6 appears.
This is because the angle is set to 1 radian, so rotating by 6 radians is almost one turn. Since 6 radians is less than 360 degrees (approximately 344 degrees), little by little the points are arranged in a spiral.
Of the significance of touching on the fun of mathematics in this way, Sanderson said, ``Certainly, by studying in textbooks and courses, you can focus more on important facts and have far fewer boring dead ends. But rediscovering these topics for yourself has a special meaning: effectively reinventing Euler's tocent function before defining it, or wondering about rational approximations before learning about continued fractions. When you learn those topics, either by getting started or by seriously examining how primes are divided among the remainder classes before you hear the name Dirichlet, you see them as familiar friends rather than as definitions that are imposed on you. I can,' he said.
Related Posts:
in Posted by log1p_kr