新型コロナウイルスの感染拡大を「感染率」「1日に出会う人の数」「移動制限」などを変更しながら直感的に理解できるシミュレーターが登場

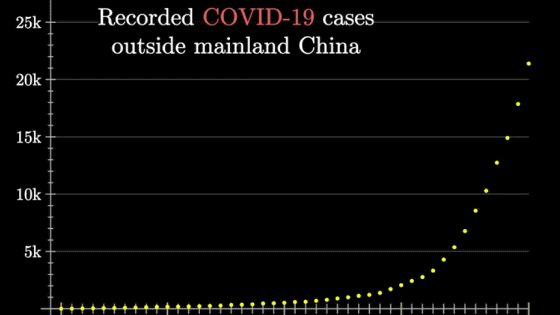
ワシントンポストに掲載された「新型コロナウイルス感染症(COVID-19)の感染拡大シミュレーション」に興味を持ったケビン・シムラー氏が、自身のブログ「Melting Asphalt」上で、新型コロナウイルスの感染拡大をよりインタラクティブなシミュレーションにバージョンアップしています。なお、シムラー氏はカリフォルニア大学バークレー校でコンピューターサイエンスの学位を取得し、マサチューセッツ工科大学(MIT)で計算言語学の博士号を取得、その後、エンジニア兼プロダクトデザイナーとして働いてきたという人物です。

Outbreak — Melting Asphalt
https://meltingasphalt.com/interactive/outbreak/

シムラー氏は自身が作成した新型コロナウイルス感染症のシミュレーターについて、「これはあくまで病気の伝播プロセスを単純化したもので、その目標は『一般的に感染がどのように展開していくか？』を学ぶことにあります。そのため、これは新型コロナウイルス感染症をモデル化する試みではありません。また、私は疫学者ではないため、いくつかの間違いがあるかもしれませんが、間違いに対してはなるべく早く修正するので、ご指摘ください」と記しています。

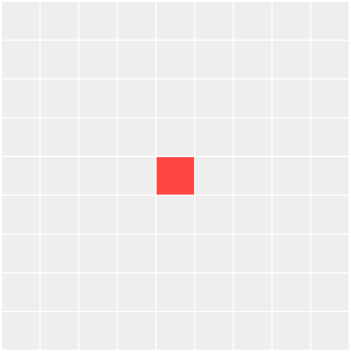
病気が最初に必要とするのは、「潜在的に病気にかかる可能性のある人々の数」です。以下の9×9コマは各コマがひとりの人を表しており、中心にある赤色のマスは感染者、その他の白色のマスは非感染者を示します。

次にこの9×9マスに時間の概念を追加します。再生ボタンをクリックすると1日ごとの感染拡大の様子が視覚的に確認できます。

「Step」をクリックすると、感染拡大の様子を1日ごとにチェック可能。1日目が感染者1名だとすると、以下が2日目。感染者数は5人に増加。

3日目。感染者の上下左右に存在するマスが続々新型コロナウイルスに感染していきます。

4日目。感染者数が増加するにつれ、1日の感染者数も指数関数的に増加していきます。

5日目。ついに9×9マスの端っこまで感染者が到達。

6日目

7日目

8日目

9日目には81マスすべてが感染してしまいました。

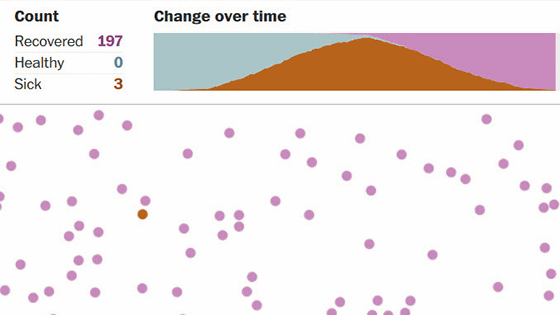
上記の画像はあくまで「感染者の増加」にだけ焦点を当てたシミュレーションです。新型コロナウイルスの死亡率は国によって大きなバラつきがあるものの比較的高い数字となっています。しかし、感染者の多くが死亡せずに回復しているのも事実です。そこで、感染者の回復まで含めて感染拡大の様子をシミュレーションすると、以下のようになります。なお、「一度感染したものの回復した人」は、感染から2日目に回復すると仮定し、回復した患者は灰色のマス目で表されます。

1日目は同じく9×9マスに1人目の感染者が発生。

2日目以降はこれまで同様に、感染者の上下左右に感染者が拡散していきます。

3日目になると、1日目の感染者が回復。中央のマス目が灰色に変わりました。

4日目以降も感染者の数と回復者の数が増加。

5日目

6日目

7日目

8日目

9日目になると9×9マスすべてが新型コロナウイルスに感染。

10日目

しかし、11日目になると9×9マスすべてが新型コロナウイルス感染症から回復しました。

新型コロナウイルス感染症に関する議論では、ウイルスに感染してから最初の症状が現れるまでの「潜伏期間」が長いとささやかれています。報道によると新型コロナウイルス感染症はこの潜伏期間中に他者にウイルスを感染させてしまうそう。そのため、自身が新型コロナウイルス感染症であることに気づかないまま、他者にウイルスを伝播させてしまう可能性があるというわけです。

潜伏期間という要素をここまでのシミュレーションに加えると以下のようになります。ただし、記事の最初に記した通り、以下のシミュレーションは新型コロナウイルス感染症の感染拡大について正しくモデル化したものではないため、潜伏期間(incubation)や症状のある日数(symptoms)が正しいとは言えません。

以下の画像は潜伏期間を「7日」、症状のある日数を「8日」に設定した場合のもので、「潜伏期間にある人」(薄い赤色)という要素が追加されています。なお、潜伏期間と症状のある日数のスライダーは共に自由に数値を変更できます。

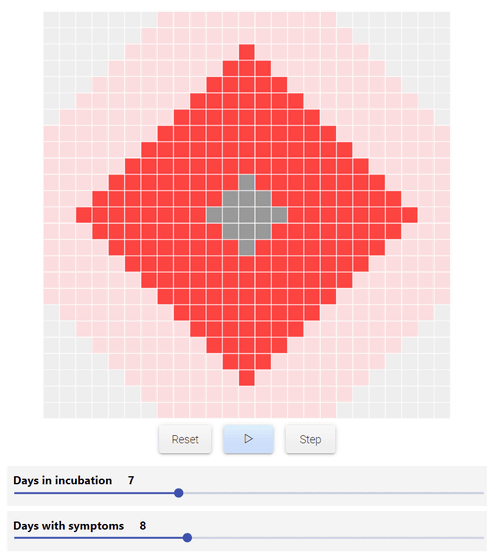
実際の病気は100％の確実性で感染していくものではないということで、感染に確率要素を追加するというのが次のステップ。

以下のシミュレーションに新たに追加されたのが感染率(Transmission rate)で、初期設定では「0.5(50％)」に設定されています。感染率という要素が追加されたことで、感染者の増加がランダムになり、感染者がきれいなひし形状に増加していくことはなくなりました。

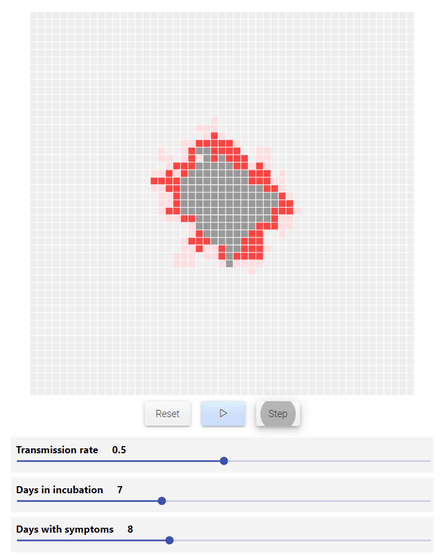
ここまでのシミュレーションでは感染者が新型コロナウイルスをうつしてしまう可能性があるのは、「4マス(4人)」だけでした。しかし、実際に1日に人と出会う数は人によって異なります。また、バスの隣に座っただけの相手と、ひとつのアイスクリームを一緒に食べた相手では感染する可能性は大きく異なるはずです。しかし、上記のシミュレーションでは感染者が1日に出会う人の数は「4人(4マス)」、感染率は「0.5(50％)」で固定となっています。これは何度も記している通り、「シミュレーションを簡単にするため」です。

続いてシムラー氏が追加したのは、感染者の移動半径(Travel radius)というパラメーター。これは潜伏期間にある感染者がパラメーターの数字分離れた場所にいる相手に新型コロナウイルス感染症をうつす可能性がある、というもの。感染者の移動を考慮して設けたパラメーターで、数字が少ないほど厳しい移動制限が設けられた状態と近くなります。ただし、1日に遭遇する人の数は「4人」で固定されたまま。

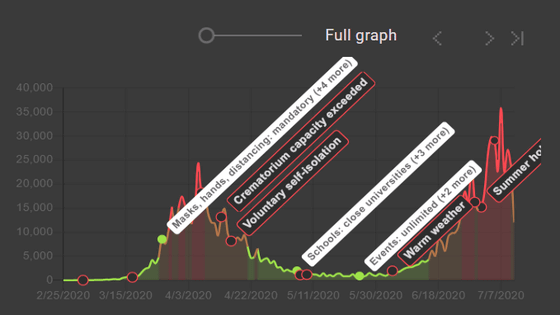
移動半径を追加したことで、感染者は格子状のマス目の中でかなりバラバラに増加していきます。マス目の下にある赤とグレーのグラフは、横軸が時間経過、縦軸が1日当たりの感染者(赤色)と回復者(灰色)の数を記したものです。

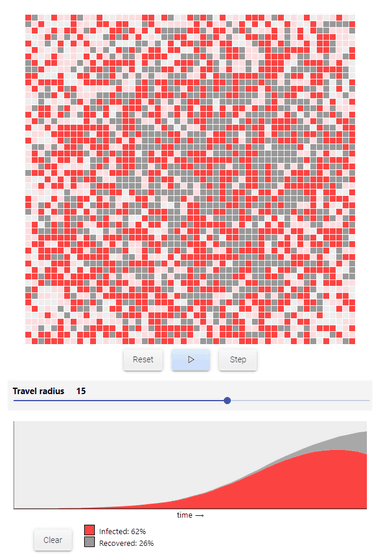
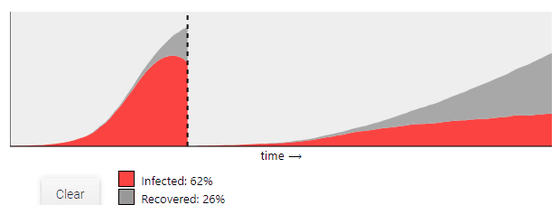
移動制限を行った場合の感染拡大がどのようになるか知りたい場合、この移動半径の数字を小さく設定すればOK。例えば以下のグラフは移動半径「15」(左)と「2」(右)での感染者・回復者数の推移を示しており、明らかに移動制限により感染者の増加が抑えられていることがわかります。

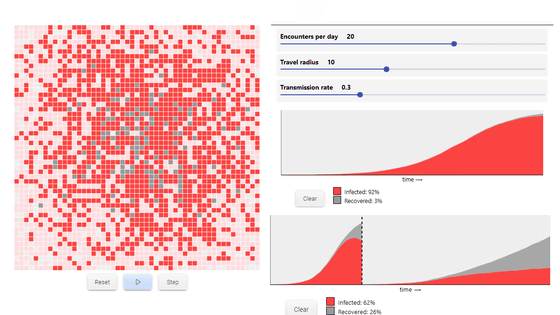
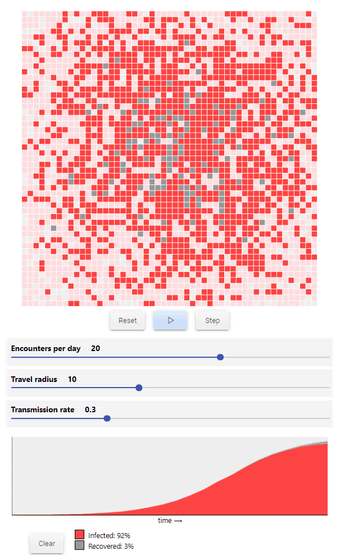
さらに、感染者が「1日に人と出会う数」(Encounters per day)まで変更できるようになると、以下の通り。1日に人と出会う数を「20人」、移動半径を「10」、感染率を「0.3(30％)」とすると、爆発的に感染が広がっていき、回復者が全体の3％という段階で感染率は92％に到達。

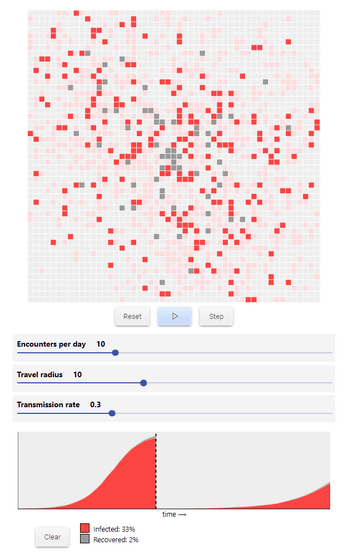
1日に人と出会う数を半分の「10人」にすると、移動半径や感染率が同じでも劇的に少ない感染率で収まることは、以下の画像を見れば一目瞭然です。同じ日数が経過しても、1日に人と出会う数を半分にするだけで劇的に感染拡大を遅らせることができます。

この「1日に人と出会う数」は、学校の閉校や公共の場での大規模集会の禁止、さらには在宅勤務の推奨といった措置を取ることで減らすことができます。そのため、シムラー氏は「NBAのシーズン中断措置にならい、あらゆる予定をキャンセルすべき」「私の理解では、これこそが新型コロナウイルスの感染拡大と戦う上で最も重要な措置です」と記しています。

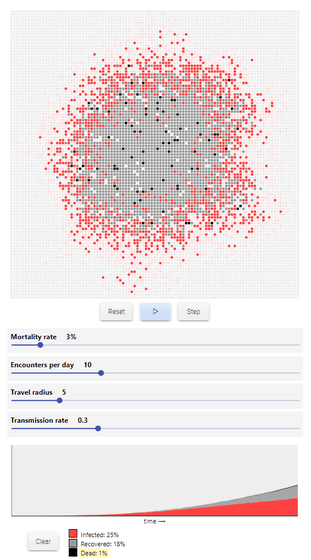
ここまでは新型コロナウイルス感染症の患者がかならず回復していましたが、死亡するというケースも存在します。新型コロナウイルス感染症の死亡率(Mortality rate)を「3％」、1日に人と出会う数を「10人」、移動半径を「5」、感染率を「0.3(30％)」とすると、シミュレーションは以下の通りになります。なお、黒色が死亡した患者を表しており、最終的な死亡率は1％です。

そして最後に追加するパラメーターが、病院の収容能力(Hospital capacity)です。これは医療機関で一度に治療できる患者の数を人口の割合で表した数字。この病院の収容能力が低いと、患者が治療を受けられなくなり、感染者の死亡率が高くなります。シムラー氏は「病院の収容能力よりも感染者数が多くなると、死亡率は2倍になる」としています。

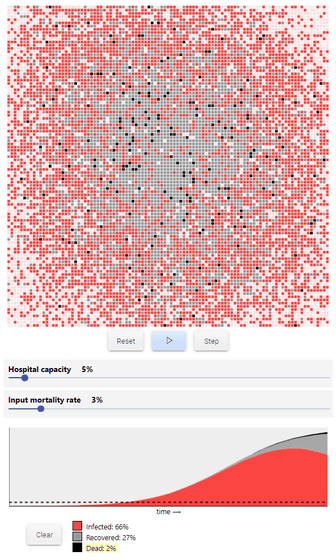
さまざまなシミュレーションを行ったシムラー氏は、「恐らく最悪のシナリオほど多くの人命を失うことはないでしょう。病院の廊下で人々が命を失うことにはならないでしょう。しかし、ウイルスが拡散し続ける限り、我々の未来には考えられない程の苦しみが待ち構えています。今日、我々が正しいことをしない限り、困難な未来が待っています。なので、旅行を止め、外出を止め、両親や友人のもとを訪れることを止め、レストランでの食事を止め、可能な限りあらゆる予定をキャンセルしてください」と記しています。