音の原理や「音色は基音と倍音によって決まる」ことがよく理解できる「Let’s Learn About Waveforms」
この世に存在する「音」は、空気や水などの物体が振動することで生み出されています。そんな「音の成り立ち」をインタラクティブに知ることができるサイトが「Let's Learn About Waveforms」です。
Let's Learn About Waveforms
http://waveforms.surge.sh/waveforms-intro
このサイトでは、実際にウェブページ上でいろいろな音を再生しながらその変化を体感する事が可能です。キーボードの「0」から「9」で音量を調整でき、「M」キーでミュートのON/OFFを切り替えることができます。その際の音量は、画面の左下に表示されます。
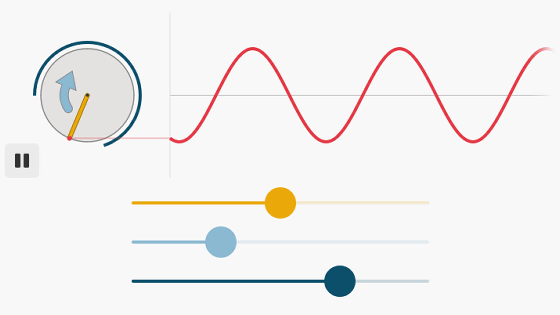
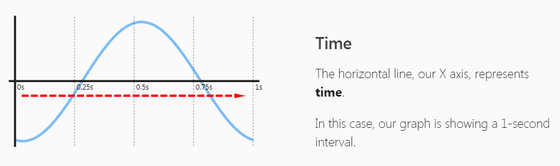
またここでは、完全に単一の周波数成分のみを持つ正弦波をもとに解説が行われます。世の中のあらゆる音は正弦波に分解することができると言われており、裏を返せば「正弦波は全ての音の源である」と言えることから、もっとも解説に適した音であるといえます。画面に表示されるグラフは、横軸が時間の長さを示し……
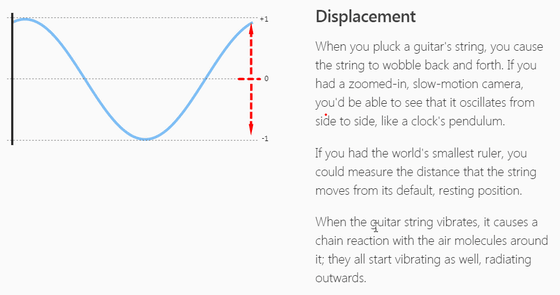
縦軸は、中心線を0として上下に波の高さが表現されます。
まずは、「音の三要素」を構成する要素の1つ、「音の大きさ」から。音の大きさは、波の高さによって変化します。音を鳴らしたまま、画面の左下にある「Amplitude」(振幅)スライダーを左方向に動かすと……
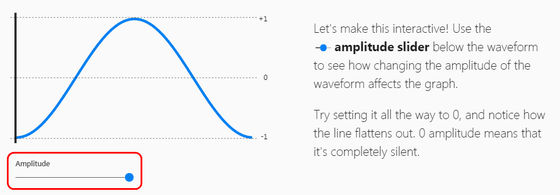
波の高さが低くなり、同時に音量も小さくなります。

スライダーを一番左まで動かすと、波が完全に消えて音も聞こえなくなりました。このように、音量は波の高さであることがわかります。

次に音の三要素の2つめである、「音の高さ」を見てみます。いま、このグラフでは「1秒間」の間に正弦波の波が2サイクル入っていることがわかります。これは、波が1秒間に2回繰り返していることを意味し、「2Hz(ヘルツ)」の音と言い表されます。

ここで読み進める前に注釈。このページでは、わかりやすさを優先するために、実際に鳴っている音の100分の1の周波数でグラフが表されています。そのため、グラフで「1Hz」と示されている場合は、実際の音は「100Hzである」と変換して読み進めてください。

先述したように、音は「波のエネルギー」となって空気などの物質を伝わってきます。音が空気中を伝播(でんぱ)する時、空中に漂う空気の分子は密度の高い部分と密度の低い部分が生まれます。この密度の差が、時速約1200kmのスピードで伝わることで、音は遠くまで届けられます。

次に、三要素の3つめである「音色」を決める「倍音」について。先述の通り、正弦波は完全に単一の周波数成分を持つ音であり、厳密には自然界には存在しないと言われています。しかし、ピアノやギターなどの楽器、街中の雑踏、人の話し声や動物の鳴き声など、全ての音はこの正弦波の組み合わせで再現することが可能です。

正弦波が含む周波数をグラフにすると、画面右下のように「1Hz」の部分にのみ棒グラフが伸びています。これは、この正弦波には1Hzの音の成分しか含まれていないことを意味しています。

次に、波形が三角形を描く三角波を見てみると、周波数成分は1Hzを最大としてその上に3Hz、5Hz、7Hz、9Hzといった音が含まれていることがわかります。この、基となる音(基音)に対して付随している周波数成分は倍音と呼ばれ、全ての音の音色を決定づける要素となっています。三角波の場合は、基音に対する倍音は3倍、5倍、7倍と奇数ばかりとなっており、これらは奇数次倍音と呼ばれます。すなわち、三角波は奇数次倍音を持つ音である、と言うことができます。

次の波形は、全て90度の角でつながる直線の集合である矩形波(くけいは)です。正弦波の正反対と言える矩形波ですが、これも全て正弦波に分解することが可能。右下のグラフで示されているとおり、矩形波は三角波と同じ奇数次倍音によって構成されていることがわかります。しかし、三角波と矩形波を聞き比べると、明らかに音色が異なることがわかります。これは両者の倍音成分の違いによって生じるもので、三角波は奇数次倍音が比較的に基音に近いところで消えていますが、矩形波は三角波よりも周波数が高い倍音を多く含んでいます。この違いが、三角波と矩形波の音の違いとして人間の耳には感じられています。

最期に、三角波に少し似たのこぎり波についてみてみます。のこぎり波の特徴は、三角波のような斜めの直線と、一瞬で波が元の位置に戻る直線の2本で構成されているところにあります。のこぎり波の場合、倍音が奇数次倍音だけではなく基音の2倍、4倍、6倍といった偶数次倍音を含んでおり、三角波や矩形波と大きく異なる特徴となっています。

実際に、音の波を合わせてみるとどうなるのでしょうか。自然界では「音の波を合わせる」などということは誰も行っていませんが、電子的に作り出した電気信号の波であれば、人工的に音の波を合わせて(=合成して)、別の音を作り出すことが可能です。

いまここに、1Hzの正弦波と3Hzの正弦波があります。この時、1Hzの波の大きさを「1」とすると、3Hzの波はその3分の1である「0.33」の大きさであるとします。実際にページを開いて音を聴いてもらうとわかりますが、1Hzの基音が100Hzの音として、そして3Hzの倍音が300Hzの音としてミックスされて聞こえます。

次に、画面に表示される「Convergence」(収束)スライダーを動かすと、2つの波が合成されて新たな形を持つ波が現れました。これが、「1Hzの基音と3Hzの倍音を持つ音」の波形というわけです。ちなみに、ここで実際に聞こえている音は基音の「ド」と、そのオクターブ上の「ソ」の音ですが、画面の表記通りであれば「ラ」とオクターブ上の「ミ」であるはず。厳密に考えると「違うじゃないか」と思ってしまいますが、そこはいい感じにスルーしておく方が良さげです。

先ほどは、「矩形波は多くの奇数次倍音を持つ音である」と言うことを述べました。ということで、実際に倍音を追加していくと、波形がどんどん角張ってきて矩形波に近くなり、それに応じて音色も変化していく様子がわかります。このように、いろいろな音色は基音と倍音の重なりのバランスによって、その特徴が決定されているということがわかります。

続いて、音にとっては切っても切り離せない「位相」について。詳細に説明すると非常に難しくなりますが、位相は周期的に繰り返す波の「ズレ」を意味する言葉で、そのズレは角度で表されます。

波の位相は360度で一周します。そのため、0度とのちょうど中間である180度にある場合の波は、完全に元の波を反転させた状態になります。

180度のズレがある状態の2本の波を合成すると、波は互いに打ち消し合って「プラスマイナス・ゼロ」の状態になります。これは、周囲の騒音を軽減する「ノイズ・キャンセリング・ヘッドホン」などにも応用されている原理です。

最後は、複数の音が重なってできる「和音」について。いま画面には3つの波が同時に表示されています。音程で表すと、黄色の波が「ド」、赤色の波が「ミ」、そして青色の波が「ソ」、つまり「ドミソ」の3和音となっています。

もとは「ド」と「ミ」と「ソ」の3つの正弦波(下図左)でできている和音ですが、それぞれの波を合成すると下図の右のような複雑な波形が作り出されます。このように、非常に複雑な波形であっても、限界まで分解していくと最後には複数の正弦波にたどり着くことができる、ということがよくわかります。

「音は基音と倍音でできている」ということがよくわかるのが以下のムービー。ここに収められている実験では、特殊な機械を使ってピアノで音を出すことで、まるで人が話しているかのような音が再現されています。普通だと考えられないような「P」や「R」の発音がピアノから聞こえるという、実に興味深い映像となっています。
Speaking Piano - Now with (somewhat decent) captions! - YouTube
・関連記事
電磁石で弦を響かせる新たな音色を手に入れたピアノ「Magnetic Resonator Piano」 - GIGAZINE
192kHz/24bitのハイレゾ無圧縮音源は本当に聴き分けられるものなのか? - GIGAZINE
「ストラディヴァリ」などの貴重なバイオリンはなぜ美しい音を奏でるのか? - GIGAZINE
MP3の「非可逆圧縮」で失われた音の残骸は不気味なゴーストサウンドだったことが判明 - GIGAZINE
電磁石で弦を響かせる新たな音色を手に入れたピアノ「Magnetic Resonator Piano」 - GIGAZINE
地球が生みだしている「謎のノイズ」の詳細が新たに判明、季節による違いはなく固有周波数も明らかに - GIGAZINE
GIFアニメでスピーカーの仕組みを解説する「How speakers make sound」 - GIGAZINE
・関連コンテンツ