"Let's Learn About Waveforms" that you can understand that the principle of sound and "tone is determined by fundamental tones and harmonics"

"Sound" existing in this world is created by vibration of objects such as air and water. A site that can interactively know such "sound formation" is "Let's Learn About Waveforms"is.

Let's Learn About Waveforms
http://waveforms.surge.sh/waveforms-intro

On this site, it is possible to experience the change while actually playing various sounds on the web page. You can adjust the volume from "0" to "9" on the keyboard, and you can switch the mute on / off with the "M" key. The volume at that time is displayed in the lower left of the screen.


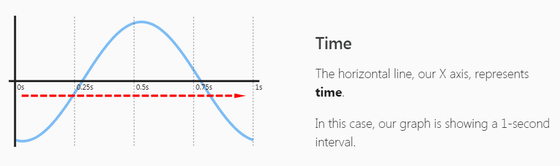
Also here we have only a single single frequency componentsine waveCommentary will be made based on. It is said that every sound in the world can be broken down into sinusoidal waves, and if you return the backside, it can be said that "a sine wave is the source of all sounds", so it is said that it is the most suitable sound for explanation I will. On the graph displayed on the screen, the horizontal axis shows the length of time ......


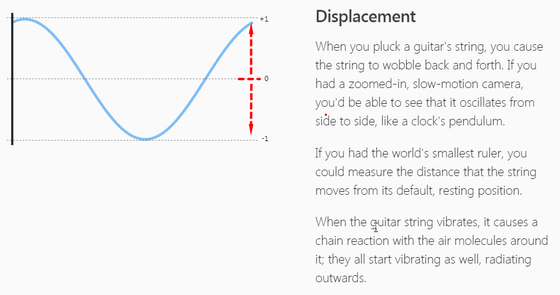
The vertical axis shows the height of the wave up and down with the center line as 0.


First, one of the elements constituting "three elements of sound", "Sound sizeFrom. The size of the sound varies with the height of the wave. Move the "Amplitude" (amplitude) slider in the lower left corner of the screen to the left while sounding ......


The height of the wave becomes lower, and the volume becomes smaller at the same time.


Moving the slider all the way to the left, the waves disappeared completely and the sounds also disappeared. In this way, you can see that the volume is the height of the wave.


Next is the second of the three elements of sound, "Sound heightI will see. Now, in this graph, you can see that two cycles of sinusoidal waves are in "1 second". This means that the wave is repeated twice per second and is expressed as "2 Hz (Hertz)" sound.


Annotation before proceeding here. In this page, the graph is represented by the frequency of 1 / 100th of the sound actually being played in order to give priority to understandability. Therefore, if it is indicated as "1 Hz" in the graph, please translate the actual sound as "100 Hz" and proceed.


As mentioned earlier, the sound becomes 'wave energy' and it travels through substances such as air. When the sound propagates through the air, molecules of air drifting in the air are born of a high density part and a low density part. This difference in density is transmitted at a speed of about 1200 km / h, so that the sound can be delivered far.


Next, the third element of the three elements "SoundAbout "overtone" that decides. As mentioned earlier, it is said that the sine wave is a sound completely having a single frequency component, strictly not in nature. However, it is possible to reproduce all sounds such as piano and guitar instruments, crowds in the streets, people's talking sounds and animal's barking with this combination of sine waves.


When plotting the frequency included in the sine wave as a graph, the bar graph extends only to the part of "1 Hz" as shown at the bottom right of the screen. This means that this sine wave contains only 1 Hz sound component.


Next, the waveform draws a triangleTriangular waveLooking at, it can be seen that the frequency component contains 1 Hz as the maximum and sounds such as 3 Hz, 5 Hz, 7 Hz, 9 Hz are included on it. The frequency component accompanying this basic sound (fundamental tone) isHarmonicIt is called an element that determines the sound of all sounds. In the case of triangular waves, the harmonics with respect to the fundamental tone are only three times, five times, seven times, and an odd number, and these areOdd order harmonicIt is called. That is, it can be said that the triangular wave is a sound with an odd order harmonic.


The next waveform is a set of straight lines all connected at a corner of 90 degreesSquare waveIt is Kukei. It is a rectangular wave that can be said to be the opposite of a sinusoidal wave, but it can also be decomposed into sine waves as well. As shown in the graph on the bottom right, we can see that the square wave is composed of the same odd harmonic overtones as the triangle wave. However, comparing the triangle wave and the rectangular wave, you can see that the timbre is obviously different. This is caused by the difference between the harmonic overtone components of the two, and the triangular wave has disappeared at the place where the odd harmonic overtone is relatively close to the fundamental, but the rectangular wave contains many overtones with higher frequency than the triangular. This difference is felt by the human ear as a difference between the triangle wave and the square wave sound.


In the end, somewhat similar to the triangle waveSawtooth waveLet's see. The feature of the sawtooth wave is that it consists of two diagonal straight lines like a triangular wave and a straight line where the wave returns to its original position in a moment. In the case of a sawtooth wave, not only odd-numbered harmonic overtones but also 2 times, 4 times, 6 times the fundamental toneEven order harmonicAnd it is a feature which is greatly different from triangular wave and rectangular wave.


In fact, what happens when you try to match the waves of sound? In nature, nobody has said that "matching sound waves" etc, but if it is a wave of electric signals produced electronically, you can artificially combine the sound waves (= synthesize) It is possible to create another sound.


Now I have 1 Hz sine wave and 3 Hz sine wave. At this time, supposing that the magnitude of 1 Hz wave is "1", the wave of 3 Hz is the size of "0.33" which is one third thereof. If you actually open the page and listen to the sound, you can hear it by mixing 1 Hz base tone as 100 Hz tone and 3 Hz harmonic as 300 Hz tone.


Next, when moving the "Convergence" (convergence) slider displayed on the screen, the two waves were synthesized and a wave with a new shape appeared. This is the waveform of "sound with 1 Hz base tone and 3 Hz harmonic overtone". By the way, the sound actually heard here is the fundamental "do" and the sound of "so" above that octave, but if it is as shown on the screen it should be "La" and "omth" on the octave . Thinking strictly, "I think it is not the same" I think, but it is better to keep it there with a good feeling.


I mentioned earlier that "a rectangular wave is a sound with many odd harmonic overtones". So, as you actually add harmonics, you can see how the waveform gets steadily angular and closer to a square wave, and the tone changes accordingly. In this way, you can see that the characteristics of various tones are determined by the balance of the overlap of the fundamental tone and the harmonic overtones.


Next, on the "phase" which can not be separated even if it is cut off for sound. Although it becomes very difficult to explain in detail, the phase is a word meaning "deviation" of the wave that repeats periodically, and that gap is expressed in degrees.


The phase of the wave goes around 360 degrees. Therefore, the wave in the case where it is 180 degrees which is just in the middle with 0 degree is the state where the original wave is completely inverted.


When synthesizing the two waves with the 180 degree gap, the waves cancel each other and become "plus / minus zero" state. This is the principle that is also applied to "noise canceling headphones" etc. to reduce ambient noises.


Lastly, about "chord" which can be made by overlapping multiple sounds. Now three waves are simultaneously displayed on the screen. In terms of the pitch, the yellow waves are "do", the red waves are "mi", and the blue waves are "so", that is, "Domiso" are three chords.


Originally it is a chord made of three sine waves ("left"), "Do", "Mi" and "So", but when synthesizing the respective waves, a complicated waveform like the right of the figure below is created . As you can see in this way, even with very complicated waveforms, at the end you can reach multiple sine waves as you break down to the limit.


The following movie can understand well that "sound is made of fundamental tones and harmonics". In the experiment included here, by using a special machine to sound with a piano, the sound as if the person is talking is reproduced. It is a very interesting image that the pronunciation of "P" or "R" that can not be considered as normal can be heard from the piano.

Speaking Piano - Now with (somewhat decent) captions! - YouTube