突然変異がどのように集団に広がり生物が「進化」するのかを「グラフ理論」で解き明かす試み

by brewbooks

チャールズ・ダーウィンが提唱した進化論では、生物に起こる突然変異を自然環境が選別し、生存に有利な方向へと進化が進むとされています。そんな突然変異の自然選択説が本当に起こりうるのかについて、ハーバード大学で進化について研究しているMartin Nowak博士が「グラフ理論」によって明らかにしています。

Mathematics Shows How to Ensure Evolution | Quanta Magazine
https://www.quantamagazine.org/mathematics-shows-how-to-ensure-evolution-20180626/

自然選択説では一度に大量の突然変異個体が登場するわけではなく、たまたま発生した「周囲の環境に有利な」突然変異が、時間をかけて集団全体に広がっていきます。そこで問題となるのが「1体の突然変異種が現れたからといって、本当に集団全体に広がるのだろうか？」という疑問です。「小さな島のように制限された範囲で繁殖する集団では、自然選択説がより顕著に現れる」といった考えもありますが、「そんなに都合よく突然変異が広まるとは思えない」と疑問を呈する人々は少なくありません。

Nowak氏は2003年に、突然変異によって発生した「明らかに生物が望まない進化」であるがん細胞がどのように体内で増殖するのかについて研究し、やがて生物の肯定的な進化である「自然選択説」にも興味を向けるようになりました。従来の生物学者らが自然選択説について明確な説明ができなかった理由について、Nowak氏は「特定の生物集団にばかり目を向けていたからだ」と考え、より一般化された自然選択説の理論を構築するべく、グラフ理論を用いた説明を試みました。

グラフ理論とは、ノード(接点)とエッジ(接点を結ぶ辺)からなるグラフに関する理論で、レオンハルト・オイラーが18世紀に理論を構築しました。Nowak氏はそれぞれの接点に生物の個体を当てはめ、辺を生物間の関係として記述しました。辺でつながる個体は交配して子孫を残し、新たに子孫の接点が接続されたり自身の接点が子孫に置き換えられる可能性を持っており、関係性の強い個体は辺に「重み」を付与して関係性を記述します。他の血統との関係が薄くなった血統種が独立して別の種となる可能性も、重み付きのグラフを用いることで記述できるとのこと。

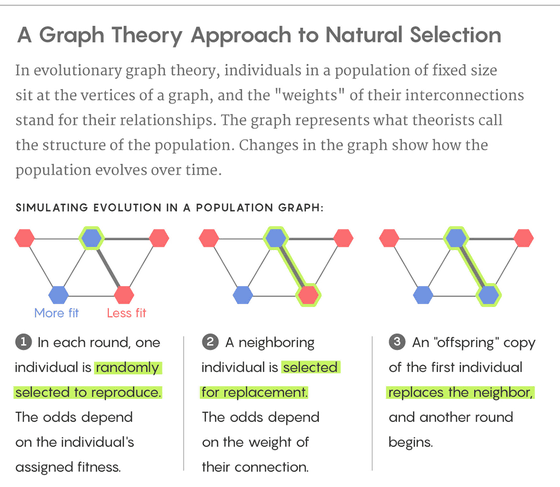
生物集団の繁殖をグラフ理論で一般化した2005年の論文で、Nowak氏は自然選択説を強化する集団の構造について説明しました。Nowak氏によれば、繁殖の方向が一方向のみに限定されている集団において、突然変異を起こした個体は一時的にその突然変異を広めることができても、最終的に通常の集団に置き換えられてしまいます。

ところが、繁殖の方向が双方向であり、グラフにすると星のような構造をしている集団では、突然変異が全体に広まることがわかったそうです。Nowak氏はこの構造を「アンプ」と表現し、アンプ状の繁殖構造を持つ生物集団は自然選択説を増強すると結論づけました。

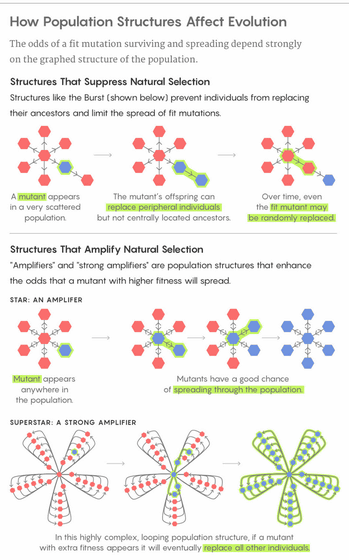
しかし、残念ながら多くの生物種においてはアンプ状の繁殖構造は見られないか、アンプ構造が証明できないほど複雑な繁殖構造を有していたとのこと。残念ながら行き詰まってしまったかに見えたグラフ理論による自然選択説の証明でしたが、2008年ごろにオーストリア化学技術研究所(IST)に勤務するコンピューター科学者のKrishnendu Chatterjee氏が、Nowak氏の理論を改善するアイデアを思いつきました。もともとグラフ理論を研究していたChatterjee氏は、グラフ理論におけるアンプがハブやループといった特定の機能を潜在的に持っていることに気づいたそうです。

Chatterjee氏がグラフ構造におけるエッジの重み付けをハブやループ構造にもとづいて変更した結果、単純な繁殖構造を有している生物集団においても、強力なアンプを作り出すことに成功しました。「重み付けを変更するだけでアンプ構造を再現できるという点は、大きな驚きでした」とChatterjee氏は語っています。

Nowak氏とChatterjee氏によれば、2人の理論が適用できるのはモデルとする生物集団が細菌および他の微生物といった、無性生殖を行う集団に限られているとのこと。有性生殖の可能性を考慮するとモデルが非常に複雑になってしまい、残念ながら有性生殖における繁殖構造をグラフ化するには至っていないと述べています。

また、進化の速度が理想的なスピードで進行するとは限らず、自然選択説以外の効果が生物の進化に関わっている可能性も考えられます。しかし、Nowak氏とChatterjee氏は強力なアンプを構築するアルゴリズムが、突然変異体の出現を促進したい細胞研究者にとって有用だと考えているそうで、今後グラフ理論を利用した生殖モデルが大きな恩恵をもたらすかもしれません。