紙を半分に折る限界はいったい何回なのか？

(Photo by Jared)

「どんな大きさ・厚さの紙であっても半分ずつに折っていくと8回で限界が来る」という俗説を聞いたことがある人は多いと思われます。いくら薄い紙であっても8回折ると厚みの合計が256倍にもなり、プレス機でもないと折り曲げることができない……というのが理由ですが、果たしてこれは本当のことなのでしょうか。

詳細は以下。
Folding Paper in Half Twelve Times

「紙を半分に折っていくと何回で限界が来るか？」という問いに対しては、例えばアメリカのMythbusters（邦題：「怪しい伝説」）など、いくつかのテレビ番組でチャレンジが行われました。

この番組ではサッカー場サイズの紙を11回折り畳むことに成功しています。

YouTube - MythBusters- Folding Paper Seven plus times

また、2001年、当時高校生だったブリトニー・ギャリヴァンさんは「ある回数紙を半分に折るために必要な紙の大きさはいくらになるか」という公式を発見。2002年には長さ1200mの特注トイレットペーパーを利用し、12回半分にすることに成功しました。

トイレットペーパーを半分ずつ折っていき、11回目に成功したブリトニーさん。

ちなみに公式はこんな感じ。厚さtの紙をn回半分に折るために必要な長さLを求めることができます。必要な長さは紙の厚さに比例するため、薄ければ薄いほど短くて済むようです。

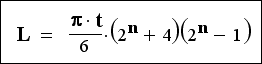
1回折るごとに厚みを半径とする半円の分だけ長さが失われていくという考え方のもと立式されたそうです。

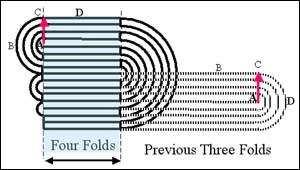
こちらは、1回前の折り目に対して直角に折る場合。厚さtの紙をn回折るために必要な正方形の紙の一辺の長さWを求められます。

ちなみに、厚み0.11mmのトイレットペーパーの場合、25回折るとだいたい富士山の高さにすることができます。

0.11mmのトイレットペーパーを何枚重ねると3776ｍになるか算出
(3 776 * 100 * 10) / 0.11 = 34,327,272.7

2の何乗でこの枚数に近づくか調べる
2^25 = 33,554,432

25回折るのに必要なトイレットペーパーの長さは

公式に値を代入
(3.14 * 0.11 * ((2^25) + 4) * ((2^25) - 1)) / 6 = 6.48143104 * 10^13

ミリメートルをキロメートルに変換
6.48143104 * 10^13 / 10^6 = 6.46143104 * 10^7

6400万キロメートルとなります。これは地球を1600周できる長さ……ちょっと用意するのは難しそうですね。