SpongeBob's N-body problem finally reaches virial equilibrium


By

Antonio Pérez

Peter Rocero, an astrophysics student at the University of La Laguna, has released an animation of a simulation of the ' N-body problem ,' a theory that says that the more celestial bodies there are, the more difficult it becomes to analyze the orbits and movements of stars. The animation shows SpongeBob Squarepants, a popular character from the animation series SpongeBob Squarepants, running the simulation.



The law of universal gravitation, which states that all objects have a mutual gravitational force, is a physical law discovered by British scientist Isaac Newton in the 17th century. By applying this law of universal gravitation, we can calculate the forces acting between celestial bodies and calculate their movements and orbits.

However, when the number of celestial bodies is three or more, this calculation becomes extremely difficult. Since it is impossible to analytically solve the equations of motion for N particles with gravity, this problem is called the 'N-body problem' in the world of astrophysics.

Rossello released an animation of 100,000 particles simulated over 5 hours and 2,000 steps. The initial positions of the N particles are in the shape of SpongeBob Squarepants.



If we simulate the motion of all particles assuming gravity, the particles move toward one point and show

gravitational collapse . On the right is a graph showing the equilibrium state of kinetic energy (Kinect Energy) and gravitational potential energy (Potential Energy), where gravitational potential energy is converted into kinetic energy.



The particles then move in a way that makes them seem to spread out and converge at two points. In terms of energy equilibrium, kinetic energy is now converted into gravitational potential energy.



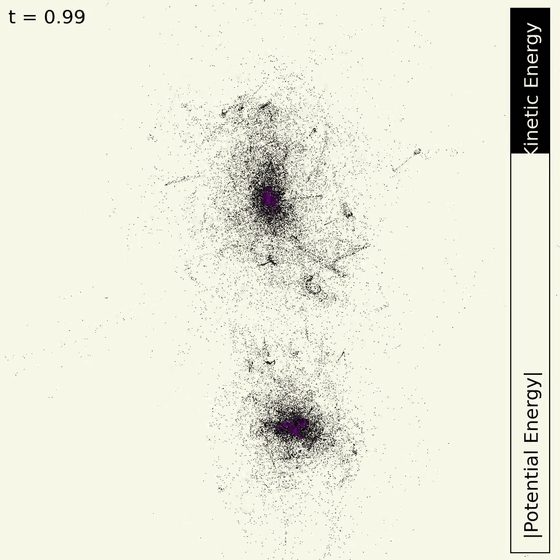
Eventually, the 100,000 particles that were SpongeBob once again concentrated at one point, eventually settling into a galaxy-like shape. The graph showing the energy balance bounces up and down, but then stops moving, indicating an equilibrium state. Rossello reports that 'N particles have reached

virial equilibrium .'



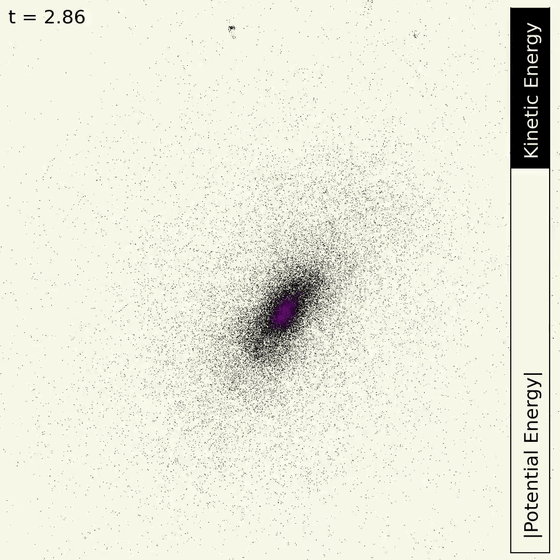
According to Rossello, the simulation is coded in Python, parallelized with numba , and plotted with Matplotlib , and the code will be hosted in his GitHub repository .

Related Posts:

in Science,   Video, Posted by log1i_yk