Movie visualizing algorithm to solve "traveling salesman problem"

ByGaël Sacré

A problem solving the problem that salesmen who move in several cities can move all cities most efficiently (with minimum movement cost)Traveling salesman problemAlthough it is called, a movie visualized by how to solve it is published on YouTube.

Traveling Salesman Problem Visualization - YouTube


For example, when there are eight cities, there are 5040 routes connecting this.


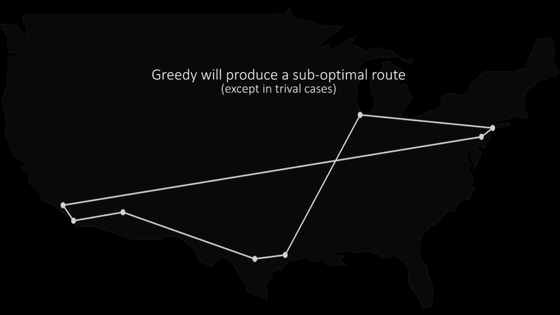
One solution is "Greedy AlgorithmA way of thinking about moving from one city to the nearest city all the time.


Although it is not "optimal", it will derive answers that are close to optimal.


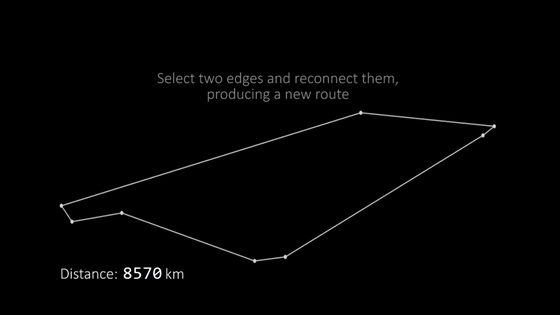
Here, the combination of using the "2-opt method". With a fairly simple algorithm, we will reconnect the two sides. At this time, if there is an overlap in the route, it resolves and creates a new route.


The answer that came out with "Greeding Law" is a little more optimized by "2-opt method".


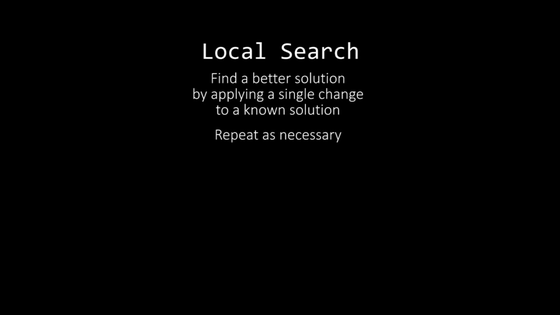
Frequently used as a search algorithm is "Local search method". Here, it seems that it refers to the hill climbing method which is its representative.


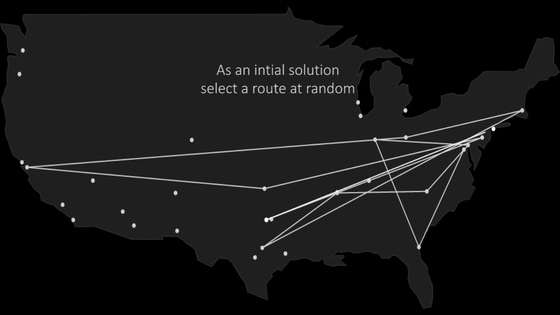
First of all, create a route randomly to some extent.


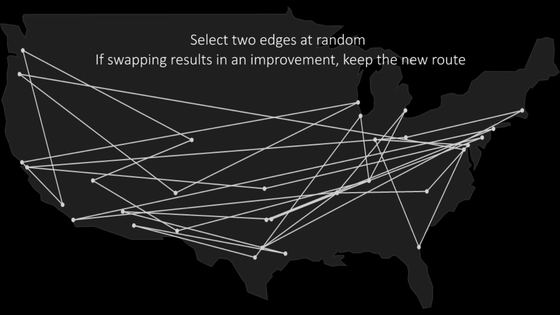
Next, we select 2 points, we will search for a better route, and if there is, we will replace it.


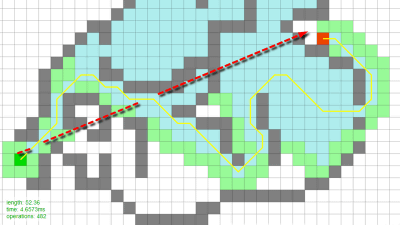
The route connecting this 32 cities is 16,592 km. Routes made by the local search method may not be able to be optimized further by "2-opt swap" ... ...


This time we could optimize slightly and we reduced it to 14,166 km.


However, there should be a more optimal route, but it is also possible to reach the "local minimum value (local minimum value)" and finish the search.


Several search algorithms have been conceived to avoid this, but one such local search method, "Annealing method(Simulated Annealing)"is.


As in the case of metal "simulated annealing", the solution is initially large because of the temperature parameter given for giving the solution, so the solution changes greatly, but as the temperature parameter gradually decreases, the solution change converges It is a mechanism that it goes. "Temp" at the lower left of the figure is the temperature parameter. At first it is big, so the solution change is also great ...


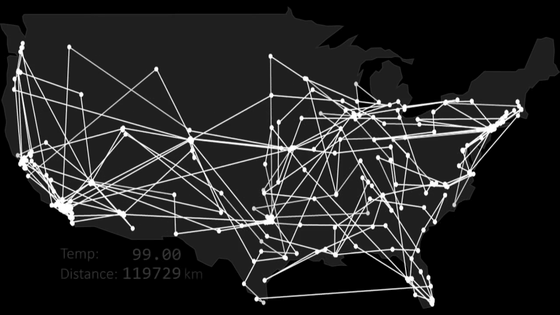
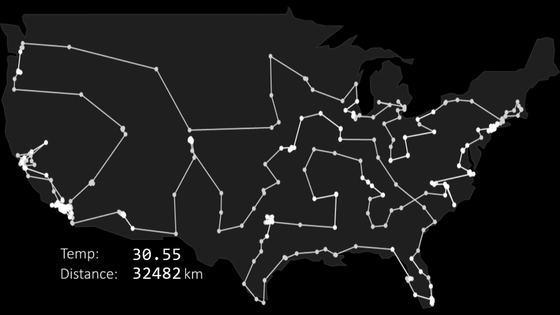
As the optimization progresses and the temperature decreases further, the range of change in solution decreases.


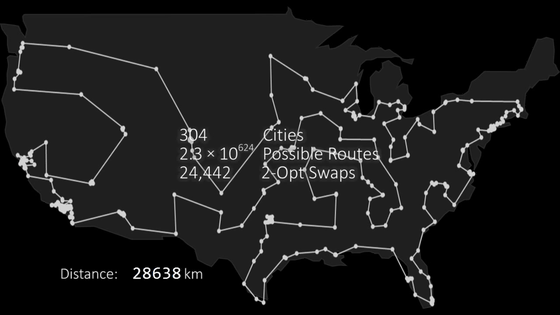
There are huge combinations of routes of "302 x 2.4 x 10" in 304 cities. In the hill climbing method, it falls into a local minimum value and can not reach the global minimum value, but if it is an annealing method it seems that better results can be obtained than the hill climbing method.