焼け焦げて穴の空いたNVIDIA RTX 5070 TiにAMD RX 580とNVIDIA RTX 2080 Tiを悪魔合体して驚異的な記録を達成

ブラジルのYouTuberであるパウロ・ゴメス氏とET's LGA1155が、焼損して基板に大きな穴が空いたNVIDIA RTX 5070 Tiを別メーカー製パーツまで流用して復活させたうえでベンチマーク記録まで更新することに成功しました。
TESTANDO A RTX 5070Ti BURACO EDITION ft. @PauloGomesVGA - YouTube

通常なら起動すら難しいほど損傷したRTX 5070 Ti搭載のグラフィックボード。雷サージによって焼けて基板に穴が空いてしまったものですが、GPUコアもVRAMも無事で、影響を受けていたのは電源供給システムだったため、ゴメス氏はAMD Radeon RX 580ボードの電源ラインと接続することで、RTX 5070 Tiのボードを動作可能に改造しています。
RTX 5070TI COM BURACO - EXPERIENCIA MALUCA DO CANAL. - YouTube

今回ゴメス氏はET's LGA1155の助けを得ながら、RTX 5070 Ti+RX 580の改造品にASUSのRTX 2080 Tiの基板をさらに組み合わせ、7時間以上かけて1枚のカードに仕上げました。
改造の途中経過では課題も多く、当初は性能がRTX 3070級にとどまり、ベンチマーク用PC側の制約でPCIe 4.0の4レーン接続しか使えなかったほか、負荷時に400mV規模の電圧降下が発生したものの、最終的には約30mVまで抑えたとのこと。
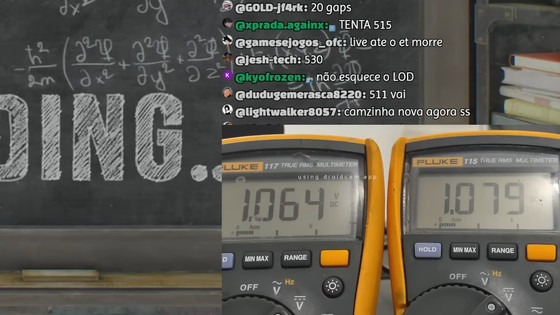
また、1080pでの表示信号の問題やドライバー競合も起き、安定化のためにRTX 2080 Ti側のPCBと元のRTX 5070 Tiの間で、電源系やグラウンドの経路に追加配線をハンダ付けしていったそうです。

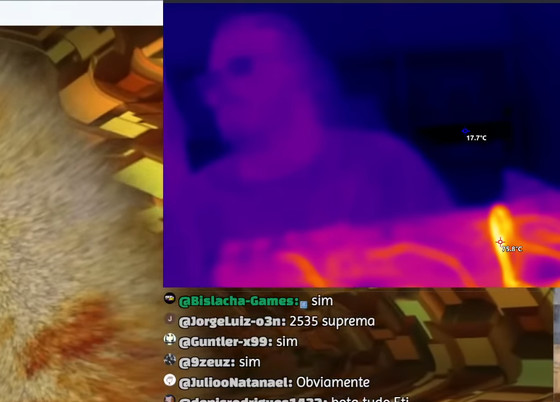
一方で熱面のリスクも顕著で、温度が50℃から80℃へ1秒で跳ね上がるスパイクが確認され、ベンチマーク中には12V配線があっという間に70度を越え、最終的にほぼ100℃に到達。そのため、ゴメス氏は「改造されたRTX 5070 Tiは一般的なゲーマーが自宅で使うのには向いていない」と評価しています。性能面の一部は別のベンチマークPCに切り替えることで改善し、PCIe 4.0の4レーンからPCIe 3.0の16レーンへ変更することで帯域が2倍になったとのこと。
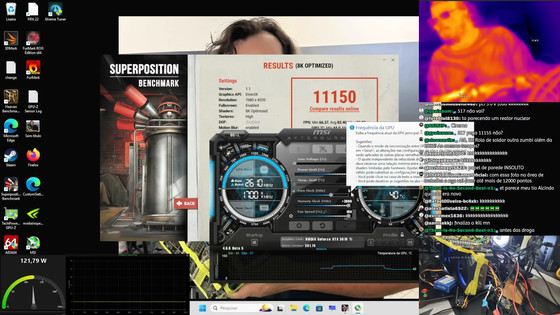
完成品は電気テープや多数のハンダ継ぎが目立つ外観で、整った改造とは言い難いものの動作自体には成功し、コアクロックは最大3.23GHz、メモリ帯域は34Gbpsに到達しました。

ベンチマーク測定にはUnigineのSuperpositionを使用。最終的にスコアは1万1150に達し、同ツール上で記録されたRTX 5070 Tiの中で首位になりました。
ハードウェア関連ニュースサイトのTom's Hardwareは「これほど物理的損傷のあるカードが動くだけでも稀で、トップ級のベンチマーク結果まで出したのは技術的な勝利だ」としつつ、再現には本格的な電気工学の知識が必要だとまとめています。
・関連記事
NVIDIAのグラボのメモリ容量を無理矢理アップグレードする方法 - GIGAZINE
中国でスクラップとして販売されていたA12Zチップ搭載の開発者向けMac miniを完全修復するムービー - GIGAZINE
Thunderbolt経由の25ギガビットイーサネットアダプターをDIYで安定させて動かす - GIGAZINE
ロシアのガジェットオタクがDDR5メモリを「自作」 - GIGAZINE
NVIDIAとAMDのマルチGPU構成で「DaVinci Resolve Studio」のベンチマーク結果を比較するとこんな感じ - GIGAZINE
・関連コンテンツ
in 動画, ハードウェア, Posted by log1i_yk
You can read the machine translated English article A burnt and holed NVIDIA RTX 5070 Ti is ….












