"Search algorithm looking at the maze" that visually enjoy the search algorithm

An algorithm to find out what kind of directions to proceed when starting point (problem) and goal (solution) is prepared is "Search algorithm"is. There are multiple types of this search algorithm, but among them, 8 basic items + game developers@ Shohei909Mr. Algorithm We tried to clear the maze with all 10 algorithms including 2 algorithms combined so that we can see what type of search will be done with eyes by "A search algorithm looking at the maze"is.

Search algorithm visualize in maze - wonderfl build flash online
http://wonderfl.net/c/hq8p

Search algorithm to see in the maze |
http://spheresofa.net/blog/?p=1044

This is the "search algorithm looking at the maze".


The operation menu like this is spread on the top of the screen ... ...


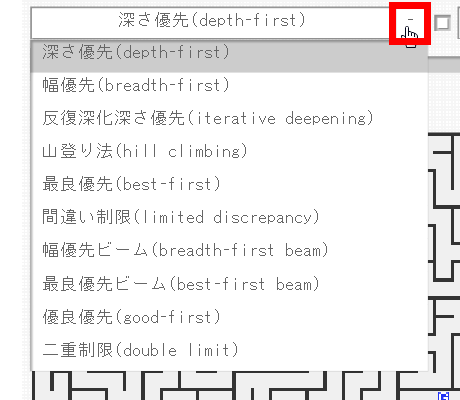
The search algorithm can be changed from the red frame part. There are 10 kinds of algorithms: depth priority, breadth first, iterative deepening depth priority, hill climbing priority, best priority, margin limitation, breadth first beam, best priority beam, superior priority, and double limit, and can be selected at any time from the top of the screen I will.


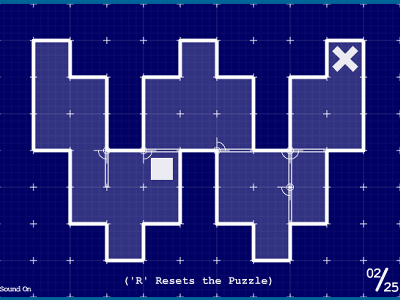
You can change the shape of the maze at any time by clicking "new", you can also adjust the "speed" and adjust the speed at which the algorithm searches for the maze.


Search is started by clicking "start". "<<" to return to the start point, "<" to return to the previous stage, ">" to go to the next stage, ">>" to the end of the search.


The blue mass marked "S" is the start point


The blue mass written as "G" is the goal point


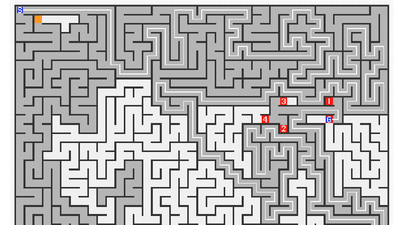
The maze itself is like this. Light gray is the unsearched part, dark gray has already been searched.


The red squirrel is a branch point found in the search or a dead end


Orange trout is a branch point and a dead end of "pruning" which was regarded as "unnecessary exploration" and was terminated, and numbers written on red squares are ranked in order of goal.


When the search ends, the road to the goal is marked with a white line on the maze. Since the dark gray portion becomes the already searched place, you can see that we did a futile wasteful search to reach the goal.


The "number of branches" and "number of times of search" are written in the lower part of the maze, and the number of searches is directly related to the number of times of movement in the maze, that is, calculation time (CPU Time). Then, the number of branches is the number of red cells found during the search, which directly leads to the amount of memory used.


The state of searching until actually clearing the maze with "depth-first search" can be seen in the following movie.

I tried using "Search algorithm looking at the maze" - YouTube


So, as each algorithm clears the same maze, I examine how much time to clear, the number of branches, the search range, etc will differ.

◆Depth-first search(Depth-first search)


Number of branches: 8, Number of searches: 803, Maximum number of branches: 15

The maximum number of branches is the largest among the 10 algorithms.

◆Breadth-first search(Breadth-first search)


Number of branches: 7, number of searches: 820, maximum number of branches: 9

It took the most number of search times among the algorithms which cleared the maze.

◆Iterative deepening depth-first search(Iterative deeping depth-first search)


Number of branches: 8, Number of searches: 775, Maximum number of branches: 12, Depth limit: 316

◆Hill climbing method(Hill climbing)


Number of branches: 0, Number of searches: 19, Maximum number of branches: 2

A search algorithm that can not clear the maze only

◆Best priority search(Best-first search)


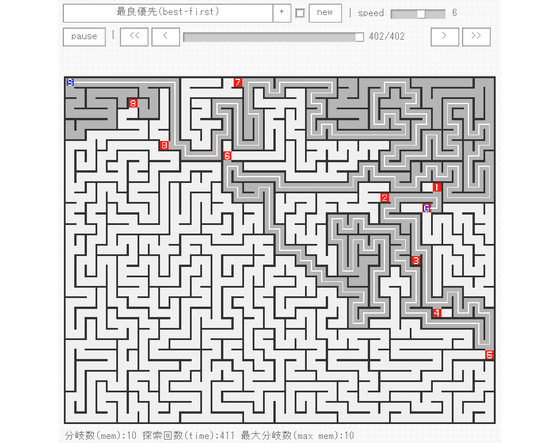
Number of branches: 10, number of searches: 411, maximum number of branches: 10

An algorithm that requires less searching frequency among 10 types.

◆Mistake limit search(Limited discrepancy search)


Number of branches: 11, Number of searches: 600, Maximum number of branches: 12, Mistakes limit: 10

The number of explorations is also relatively small here. However, the number of branches is the largest among the algorithms that cleared the maze.

Breadth-first beam search(Breadth-first beam search)


Number of branches: 5, number of searches: 682, maximum number of branches: 7

Only the number of branches is minimum.

◆Best priority beam search(Best-first beam search)


Number of branches: 5, Number of searches: 394, Maximum number of branches: 6

In clear of the maze, both the number of search and the number of branches are minimum.

◆ Excellent Priority Search(Good-first search)


Number of branches: 7, number of searches: 814, maximum number of branches: 8

◆ Double restriction search(Double limit search, Good-first beam search)


Number of branches: 7, Number of searches: 809, Maximum number of branches: 8

Routes to search maze by search algorithms seem to differ considerably, depending on the shape of the maze, the shape of the searched zone will change greatly. In addition, the search algorithm used in the "search algorithm looking at the maze" can be used not only for the maze but also for searching for games such as puzzles and solitaire, and apply it to fighting games such as chess and Othello if you add your hands It is possible to do.