How to practice the 'Socratic method' that develops logical thinking by repeatedly asking questions?

by Bob Cotter

The Socratic method is a method of repeatedly asking questions about a topic without telling the other person anything, stimulating their curiosity and gradually progressing their understanding of the topic in a logical manner. This method allows people to learn about complex topics with their own thoughts and insights, and can help them acquire advanced thinking skills. An experiment was conducted to demonstrate that even children can understand difficult topics using the Socratic method.

The Socratic Method
http://www.garlikov.com/Soc_Meth.html

Richard Garlikov, a professor of ethics and philosophy at Troy University in Alabama, conducted an experiment using the Socratic method in a third-grade class at a suburban elementary school. With two weeks left until summer vacation, the students were anxious and had difficulty concentrating on complex, theoretical learning. The experiment was designed to teach teachers how to use the Socratic method in their lessons and how to keep students engaged in class. While the ostensible theme of the lesson was to teach students binary arithmetic through questioning, the real goal was to demonstrate the usefulness of the Socratic method to teachers. While only two or three students initially understood the lesson, the students enjoyed the lesson, and 19 of the 22 students fully understood the material.

The class proceeded by alternating between questions from Mr. Garlikov and answers from the students, with 76 questions and answers exchanged over the course of 25 minutes.

◆01: (holding up 10 fingers) How many do you have?
10 pieces

◆02: What happens if you write '10' on the blackboard?
One of the students writes '10' on the board.

◆03: What are other ways to express “10”?
Another student draws 10 lines

◆04: What are other ways to express “10”?
Another student divides the sheet into five lines and fills it in.

◆05: What are other ways to express “10”?
Another student writes '2 x 5'

◆06: There are many ways to write the number 10, but is there a way to write it that means '10' itself?
TEN

◆07: Anything else?
X (Roman numeral 10)

◆08: (pointing at the word 'TEN') What is this?
The word 'TEN'

◆09: How is this word written?
character

◆10: How many letters are there in the alphabet?
26 characters

◆11: How many words can you make using the alphabet?
countless

◆12: (pointing at the number '10') What is this number represented using?
numeral

◆13: How many number words are there?
9 or 10

◆14: 9 or 10?
10 pieces

◆15: What happens when you count numerals starting from zero?
0, 1, 2, 3, 4, 5, 6, 7, 8, 9

◆16: How many numbers can you make using number words?
Infinite, countless, many

◆17: Why are there 10 numbers? Is it because we have 10 fingers?
Maybe so

◆18: What if aliens only had two fingers? How many numerals would they have?
2 pieces

◆19: How many numbers can you express using two numerals?
Not that many.
(A student) has trouble representing numbers.

◆20: What's the problem?
Unable to make the number 7 using seven fingers

◆21: How do you say “55”?
Hold up five fingers, put them down, and raise them again

◆22: That way of doing things might represent '10'?
The student falls silent and says, 'Hmm...'

◆23: Now let's see what you can do with just two fingers. We have number words 0 through 9, but if you only had two number words, which ones would they be?
0 and 1

◆24: What happens when you count numbers using these number words?
0, 1 (After counting to two, the classroom falls silent)

◆25: Is that all? If there are nine numerals, how do you represent numbers greater than nine?
Student writes '1 0'

◆26: Why is it expressed like this?
This is how you write '10'

◆27: What do you do if you have used a number word once and want to use the same number word twice?
Write 1 in a separate digit

◆28: When writing '1 0', what do you call the digit that contains '1'?
10 digits

◆29: Why do you call it that?
I don't know

◆30: What does it mean when there is a '1' in the tens digit and a '0' in the ones digit?
One 10

◆31: Why does this mean 10? Why is the tens digit called 'tens digit'?
I don't know, but that's it

◆32: If there are 9 numerals, which number needs a new digit?
10

◆33: Maybe that's why it's called the 'tens digit'? What number needs the next new digit?
100

◆34: What is that digit called?
100 digits

◆35: How do you write '20' after '19'?
Change 9 to 0 and 1 to 2

◆36: So that means there's one 20. Because there are two tens?
20

◆37: What number requires a fourth digit?
1000

◆38: What is that digit called?
1000 digits

◆39: Now, let's go back to two-finger arithmetic. What if you want to represent '2' after '0' and '1'?
Create a new digit

◆40: What should we call that digit?
Two digits?

◆41: That's right! Because the number that needs a new digit is '○○.' What number goes in '○○'?
2

◆42: What number goes in the second digit?
1

◆How many are left in 43:1?
There is no remaining

◆44: So '2' is represented as '10'?
Yes, it looks the same as '10(TEN)'.

◆45: No, it's just you who see it that way, but to two-fingered aliens, this is '2.' If you only had two fingers, how long would it take you to learn multi-digit numbers?
It will take some time

◆46: When you see '1 0,' were you taught to read it as 'juu' instead of 'ichi, zero'?
I learned

◆47: So let's try a different approach here. How do you read '1, 0'?
2

◆48: It's a little difficult, isn't it?
yes

◆49: Let's get used to it, just like an alien child learning numbers for the first time. What number comes after 2?
3

◆50: How do you say “3”?
One 2's digit and one 1's digit

◆51: So, you represent 0 to 3 using '0,' '1,' '10,' and '11.' How do you represent '4'?
Create a new digit

◆52: What should we call that digit?
4 digits

◆53: How do you express the number '4'?
100

◆54: How do you represent “5” next?
101

◆55: So how do you represent '6'? What do you put in the ones digit?
1

◆56: How do you say '6'?
110

◆57: How does '110' become '6'? What is this number made of?
One 4 digit and one 2 digit

◆58: So what does 'one 4 digit and one 2 digit' represent?
6

◆59: Next, how do you represent “7”?
111

◆60: We've run out of numbers again. How do we represent '8' through '10'?
Add a new digit: 8 is '1000', 9 is '1001', and 10 is '1010'.

◆61: So, how many numbers can be represented using 1 and 0?
It can be done infinitely

◆62: Let's look at another number. Can we simplify multiplication using Roman numerals? For example, 'MCXVII times LXXV'?
It's not easy

◆63: Let's look at the case of a two-fingered alien. Let's calculate '2 times 3' using the usual method.
10 x 11 = 110

◆What does 64:110 represent?
6

◆65: What is 2 multiplied by 3 in the usual way?
6

◆66: It seems like alien math is the same as our math?
Seems the same

◆67: Rather than being the same, it only uses the numbers 0 and 1, so the calculation is easier, right?
easy!

◆68: I understand how to do the calculations, but until I get used to it, it's difficult to quickly read long numbers like '10011001011,' right?
yes

◆69: So who uses this counting method?
No one uses it, aliens use it

◆70: Think about the things around you. When do you use this counting method?
Not in use

◆71: No, I do. Can you think of anything?
I can't think of anything

◆72: (pointing at the light switch) What is this?
switch

◆73: (Turn the switch on and off several times) How many positions can you move the switch to?
2

◆74: What do you call these positions?
On and off, up and down

◆75: What if you were to assign a number?
1 and 2
(One student says) Ah! 0 and 1!
(Everyone realizes) That's right! 0s and 1s!

◆76: That's right. This concludes the experiment.

After the final question, Garlikov explained that computers and calculators operate on the binary system, and that there are other systems, such as the quinary system and the duodecimal system, which subtract or add numbers. He then explained that he used the Socratic method to guide the lesson, saying, 'You may think I've taught you something you didn't know today, but I've only asked you questions, not taught you anything. Because you all knew everything before class. Keep studying hard.' According to Garlikov, the children participated in the lesson as a united group, without getting bored or losing focus. Afterward, the children continued to talk enthusiastically with their teachers until it was time to go home.

Garlikov explains the usefulness of the Socratic method, saying, 'Classes using the Socratic method require time to prepare, and they are not applicable to all topics, but when used well, it allows students to experience the joy and pleasure of exploring complex ideas on their own, and it can help teachers transform passive students into creative, bright students. It is a method that allows both students and teachers to learn with concentration.'

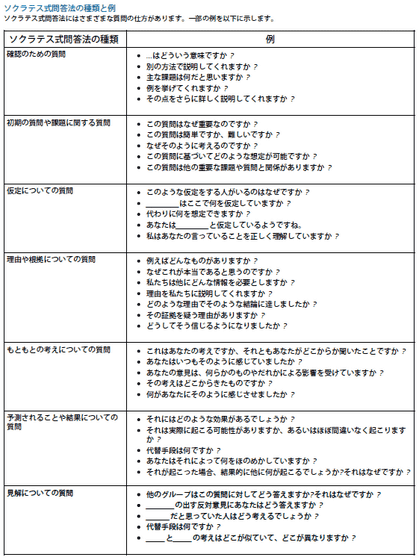
An example of an actual application of the Socratic method is as follows: 'Where does that idea come from?' 'Why did you come to believe that?' 'What are the alternatives?' These are questions that could be used in conversations between multiple people or for asking yourself questions.