質問を繰り返すことで論理的な考え方を身につける「ソクラテス式問答法」の実践方法とは？

by Bob Cotter

あるテーマについて相手に何も伝えずに質問を繰り返していくことで、相手の好奇心を刺激して、テーマについての理解を論理的にだんだんと進めていく「ソクラテス式問答法」という方法がありますが、これは複雑なテーマについて自身の考えと洞察をもって学ぶというやり方で、高度な思考スキルを身につけることができます。このソクラテス式問答法を使えば子どもも難しいテーマを理解できることを実証する実験が行われました。

The Socratic Method
http://www.garlikov.com/Soc_Meth.html

アメリカ・アラバマ州のトロイ大学で倫理学や哲学を教えているRichard Garlikov氏は、郊外の小学校の3年生のクラスで、ソクラテス式問答法を使った実験を行いました。夏休みまで残り2週間ということで子どもたちはそわそわしており、複雑で理論的な学習には集中しにくい時期でした。この実験は、ソクラテス式問答法を使った授業の進め方と、子どもたちを授業に集中させる方法について、学校の教師たちが学ぶために行われ、授業の表向きのテーマは生徒たちに二進法の計算について質問形式で教えていくことでしたが、教師にソクラテス式問答法の有用性を知ってもらうことが本題でした。授業内容について最初から理解していた子どもはほんの2～3人でしたが、子どもたちは楽しみながら授業に参加して、22人のうち19人が授業内容をすべて理解したとのこと。

授業はGarlikov氏からの質問と生徒たちからの回答を交互に繰り返すことで進められていき、25分間で76個の質問と回答が行われました。

◆01：(指を10本出しながら)いくつありますか？
10本

◆02：「10」を黒板に書いて表してみたらどうなりますか？
生徒の1人が黒板に「10」と記入

◆03：その他に「10」を表す方法は？
別の生徒が線を10本記入

◆04：その他に「10」を表す方法は？
別の生徒が線を5本ずつに分けて記入

◆05：その他に「10」を表す方法は？
別の生徒が「2×5」と記入

◆06：「10」を表す書き方はたくさんありますが、「10」そのものを意味する書き方はありますか？
TEN

◆07：他には？
X(ローマ数字の10)

◆08：(「TEN」という単語を指さしながら)これは何ですか？
「TEN」という単語

◆09：この単語は何を使って書かれていますか？
文字

◆10：アルファベットは何文字ありますか？
26文字

◆11：アルファベットを使って単語をいくつ作れますか？
無数

◆12：(「10」という数字を指さしながら)この数字は何を使って表されていますか？
数詞

◆13：数詞はいくつありますか？
9個か、10個

◆14：9個か、10個か、どちらですか？
10個

◆15：数詞をゼロから数えてみると？
0, 1, 2, 3, 4, 5, 6, 7, 8, 9

◆16：数詞を使って数字をいくつ作れますか？
無限、無数、たくさん

◆17：どうして数詞は10個なのでしょうか？指が10本あるからでしょうか？
そうかもしれない

◆18：もしも宇宙人が2本しか指を持っていなかったら？数詞はいくつあるでしょうか？
2個

◆19：2つの数詞を使って、いくつの数字を表すことができますか？
そんなに多くない。
(ある生徒が)数字を表すのに問題がある。

◆20：何が問題ですか？
指を7本使って「7」を表すことができない

◆21：君は「55」はどうやって表しますか？
5本の指を挙げて、一度下ろして、もう一度挙げる

◆22：そのやり方は「10」を表しているかもしれないですね？
生徒は「うーん……」と黙り込んでしまう

◆23：それでは、2本の指だけで何ができるか見ていきましょう。数詞は0から9までありますが、もし数詞が2つしかないとしたら、どの数詞ですか？
0と1

◆24：これらの数詞を使って数字をかぞえてみると？
0、1(2つだけかぞえたあと、教室は静まりかえる)

◆25：それだけですか？数詞が9個の場合、9以上の数字を表すにはどうしますか？
生徒が「1 0」と記入

◆26：なぜこのように表すのですか？
これが「10」を表す書き方だから

◆27：数詞を1度使ってしまった場合、同じ数詞を2度使いたい場合はどうしますか？
1を別のケタに書く

◆28：「1 0」と書いたときに「1」の入っているケタを何と呼びますか？
10のケタ

◆29：どうしてそのように呼ぶのですか？
わからない

◆30：10のケタに「1」、1のケタに「0」が書かれているときにはどういう意味になりますか？
10がひとつ

◆31：どうしてこれが10という意味になるのですか？どうして10のケタは「10のケタ」なのですか？
分からないけれど、そういうもの

◆32：9個の数詞がある場合、新しいケタが必要になる数字は？
10

◆33：それが理由で「10のケタ」と呼ぶのではないでしょうか？次の新しいケタが必要になる数字は？
100

◆34：そのケタは何と呼ばれていますか？
100のケタ

◆35：「19」の次に「20」と書くにはどうしますか？
9を0に、1を2に変える

◆36：つまり20がひとつ、という意味ですね。なぜなら10が2つあると？
20

◆37：4つ目のケタが必要になる数字は？
1000

◆38：そのケタは何と呼ばれていますか？
1000のケタ

◆39：それでは2本指の算数に戻ります。「0」と「1」の次に「2」を表したい時にはどうしますか？
新しいケタを作る

◆40：そのケタは何と呼べばいいでしょうか？
2のケタ？

◆41：その通り！なぜなら新しいケタが必要になる数字が「○○」だからです。「○○」に入る数字は？
2

◆42：2のケタに入れる数字は何ですか？
1

◆43：1はいくつ余っていますか？
余っていない

◆44：それでは「2」は「10」と表すのですね？
はい、見た目は「10(TEN)」と同じ

◆45：いいえ、そのように見えているのは君たちだけで、2本指の宇宙人にとってはこれが「2」です。もし指が2本しかなかったら、いくつものケタがある数を学ぶためにはどのくらいの時間がかかりますか？
少し時間がかかる

◆46：「1 0」と書いてあるときに「いち、ぜろ」ではなく「じゅう」と読むように習いましたか？
習った

◆47：では、ここでは違う風に教えましょう。「1, 0」は何と読みますか？
2

◆48：少し難しいですね？
はい

◆49：宇宙人の子どもが初めて数を学ぶように、慣れていきましょう。2の次にくる数字は？
3

◆50：「3」をどのように表しますか？
2のケタがひとつと、1のケタがひとつ

◆51：ということは、「0」「1」「10」「11」というように0から3を表していますね。「4」を表すにはどうしますか？
新しいケタを作る

◆52：そのケタを何と呼びましょうか？
4のケタ

◆53：「4」を表す方法は？
100

◆54：次に「5」を表すには？
101

◆55：それでは「6」はどうやって表しますか？1のケタには何を入れますか？
1

◆56：「6」を表す方法は？
110

◆57：どうして「110」が「6」になるのでしょうか？この数字は何でできていますか？
4のケタがひとつと、2のケタがひとつ

◆58：つまり「4のケタがひとつと、2のケタがひとつ」で何を表しますか？
6

◆59：次に「7」を表すには？
111

◆60：また数字を使い切ってしまいました。「8」から「10」を表すには？
新しいケタを増やす。8は「1000」、9は「1001」、10は「1010」。

◆61：それでは、1と0を使っていくつの数字を表すことができますか？
無限にできる

◆62：ここで別の数字を見てみましょう。ローマ数字を使ってかけ算を簡単にできますか？例えば「MCXVIIかけるLXXV」は？
簡単にできない

◆63：2本指の宇宙人の場合を見てみましょう。「2かける3」を普段の計算方法でやってみましょう。
10×11＝110

◆64：110は何を表していますか？
6

◆65：2かける3を普段通りに計算するといくつですか？
6

◆66：宇宙人の算数と私たちの算数は同じみたいですね？
同じみたい

◆67：同じというよりも、使っている数字は0と1だけなので、計算はもっと簡単ですね？
簡単！

◆68：計算のやり方は分かったけれど、慣れるまでは「10011001011」のような長い数をさっと読むのは難しいですね？
はい

◆69：それではこの数え方を誰が使っていますか？
誰も使っていない、宇宙人が使う

◆70：身の回りのものについて考えてみてください。この数え方をいつ使っていますか？
使っていない

◆71：いいえ、使っています。何か思いつきませんか？
思いつかない

◆72：(電灯のスイッチを指さしながら)これは何ですか？
スイッチ

◆73：(何度かオン・オフを繰り返して)スイッチを動かす位置はいくつありますか？
2

◆74：これらの位置のことを何と呼びますか？
オンとオフ、上と下

◆75：数字を割り当てるとしたら？
1と2
(ある生徒が)あ！0と1だ！
(全員が気づいて)そうだ！0と1だ！

◆76：その通り。これで実験は終わりです。

最後の質問のあとに、Garlikov氏はコンピュータや計算機が二進法で動いていることや、二進法のほかにも数詞を減らしたり増やしたりした「五進法」「十二進法」などがあることを伝えてから、「ソクラテス式問答法」を使って授業を進めたことを明かして「今日は私が君たちに知らないことを教えた、と思っているかもしれないが、私は質問を繰り返しただけで何も教えていません。なぜなら君たちが授業の前にすべてを自分で知っていたからです。これからも勉強をがんばってください」と言って授業を終えました。Garlikov氏によると、子どもたちが飽きたり集中力をなくしたりすることなく、クラス全員で一丸となって授業に参加していたそうです。その後、子どもたちは下校時間まで熱心に教師たちと話し続けたとのこと。

Garlikov氏は「ソクラテス式問答法を用いた授業は準備に時間がかかり、あらゆるテーマに適用できるというわけではありませんが、うまく使うことができれば、生徒は複雑なアイデアを自分自身で探究していく喜びや楽しみを得ることができ、また、教師は受け身になりがちな生徒たちを創造力に富んだ明るい態度に変えることができるという、生徒と教師の両方が集中して学ぶことができる方法だ」とソクラテス式問答法の有用性を説いています。

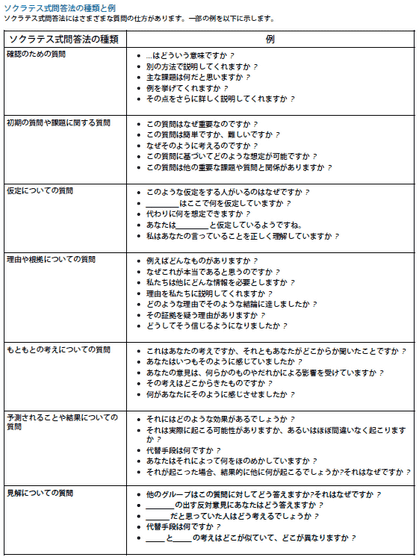
実際にソクラテス式問答法を適用している実例は以下のような感じで、「その考えはどこからきたものですか？」「どうしてそう信じるようになりましたか？」「代替手段はなんですか？」など、複数人同士の対話や、自身への自問にも使えそうな質問となっています。

効果的プロジェクトの設計 : 発問　ソクラテス式問答法