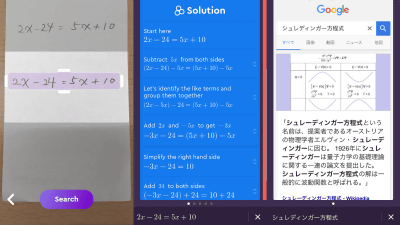
AI successfully solves unsolved math problem almost automatically, a major advance in AI tools

Paul Erdős , known as the most prolific mathematician of the 20th century, proposed many unsolved problems throughout his life, known as 'Erdős problems.' GPT-5.2 Pro solved one of these problems, and renowned mathematician Terence Tao commented, 'To our knowledge, this is a near-autonomous solution that has not been reproduced in existing literature, and it represents a real improvement in AI capabilities.'

How We Used GPT-5.2 to Solve an Erdos Problem : r/singularity
https://www.reddit.com/r/singularity/comments/1q6vaxj/how_we_used_gpt52_to_solve_an_erdos_problem/

AI contributions to Erdős problems · teorth/erdosproblems Wiki · GitHub
https://github.com/teorth/erdosproblems/wiki/AI-contributions-to-Erd%C5%91s-problems

Erdős Problem #728
https://www.erdosproblems.com/728

The topic of this issue, Erdős Problem 728, is a number theory problem about the divisibility of factorials proposed by Erdős et al. in 1975. It asks, 'For sufficiently small constants C and ε, are there infinitely many integers (a, b, c) such that 'a!b! divides n!(a+bn)!' and 'a+b is greater than n+C*log n'?' However, according to Tao, the original problem statement was ambiguous, and it was unclear, for example, whether the constant C was intended to be a small or large constant.

AI tools GPT-5.2 Pro and Aristotle played a leading role in solving this problem.

Reddit user ThunderBeanage has attempted mathematical proofs using various LLMs. However, according to ThunderBeanage, when traditional LLMs are allowed to search the internet, they sometimes realize the problem is unsolved, conclude it's 'unsolvable,' and stop searching for a solution. He has therefore tried prompting the LLM to not search the internet, or blocking the internet to avoid this behavior. Furthermore, ThunderBeanage says that even when he blocked the internet, hallucinations and fatal leaps frequently occurred, preventing his proofs from being correct, which was a major obstacle.

However, when GPT-5.2 Pro, released in December 2025, encountered a lemma that could not be fully resolved during the proof creation process, it tended to honestly state 'this is unsolved' without forcing it to be invented, and the overall framework was correct for a significant percentage of cases. Therefore, ThunderBeanage ultimately devised a method: 'Using GPT-5.2 with a network to organize the intent and direction of the problem and create a short prompt written in LaTeX,' then 'having another instance of GPT-5.2 write a proof using that prompt with the network disabled,' and then 'having the other instance verify and correct the calculation.'

On January 4, GPT-5.2 Pro output a constrained proof. However, due to the ambiguity of the problem, this was not considered to be a correct solution, so the solution was reinterpreted with a stricter condition: a, b ≤ (1-ε)n.

ChatGPT - Erdos factorial divisibility
https://chatgpt.com/s/t_695bdbf3047c8191af842d03db356b1a

A user named AcerFur passed this to Aristotle, who formalized it in Lean. However, a debate then erupted within the community, and it became necessary to impose stricter constraints on how the constant C should be interpreted.

So, ThunderBeanage asked GPT-5.2 Pro again whether it could upgrade the argument to satisfy the additional constraints, and GPT-5.2 Pro answered yes. The resulting proof was then formalized by Aristotle. Although the proof contained small errors, Aristotle automatically repaired the gaps and refined it to a Lean-verified form.

Factorial Divisibility Beyond the Logarithmic Barrier /Erdos728Updated.pdf - Google Drive
https://drive.google.com/file/d/1xRw8_o2C8HwmxMDnBR5OJlxXaW7jlYbz/view

Tao, who is currently working on the Erdős problem, praised the proof, saying, 'The AI solved the Erdős problem almost autonomously.' He particularly found it intriguing that the AI was able to reach a conclusion not found in existing literature, and that it was able to improve the paper by filling in gaps and correcting references through additional instructions and repeated dialogue, allowing it to rewrite and improve the paper multiple times in a short period of time.

Tao believes that it is preferable for humans to take the lead in writing the important parts, but he highly values the fact that in the past, it took a lot of effort just to produce a single, readable manuscript, and subsequent revisions tended to be limited to localized corrections.However, with AI, it is possible to quickly and repeatedly rewrite a document, including making major structural changes.