Dec 25, 2024 09:45:00

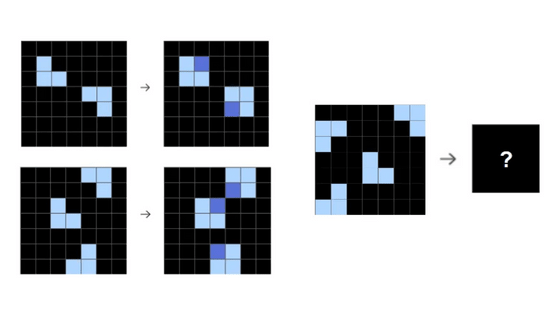
Mathematicians talk about the shock of OpenAI's o3 model scoring 25.2% on the ultra-difficult math dataset 'FrontierMath'

Kevin Buzzard, a mathematician and professor of pure mathematics at Imperial College London, posted a blog post explaining how OpenAI's o3 model scored 25.2% on the FrontierMath problem dataset.

Can AI do maths yet? Thoughts from a mathematician. | Xena

https://xenaproject.wordpress.com/2024/12/22/can-ai-do-maths-yet-thoughts-from-a-mathematician/

On December 20, 2024, OpenAI announced a new inference model, the o3 series. OpenAI said the o3 model has the 'most advanced inference capabilities ever developed,' and is preparing for its release in 2025.

OpenAI announces 'o3' series with significantly enhanced inference capabilities, introducing a mechanism to 'reconsider' OpenAI's safety policy during inference - GIGAZINE

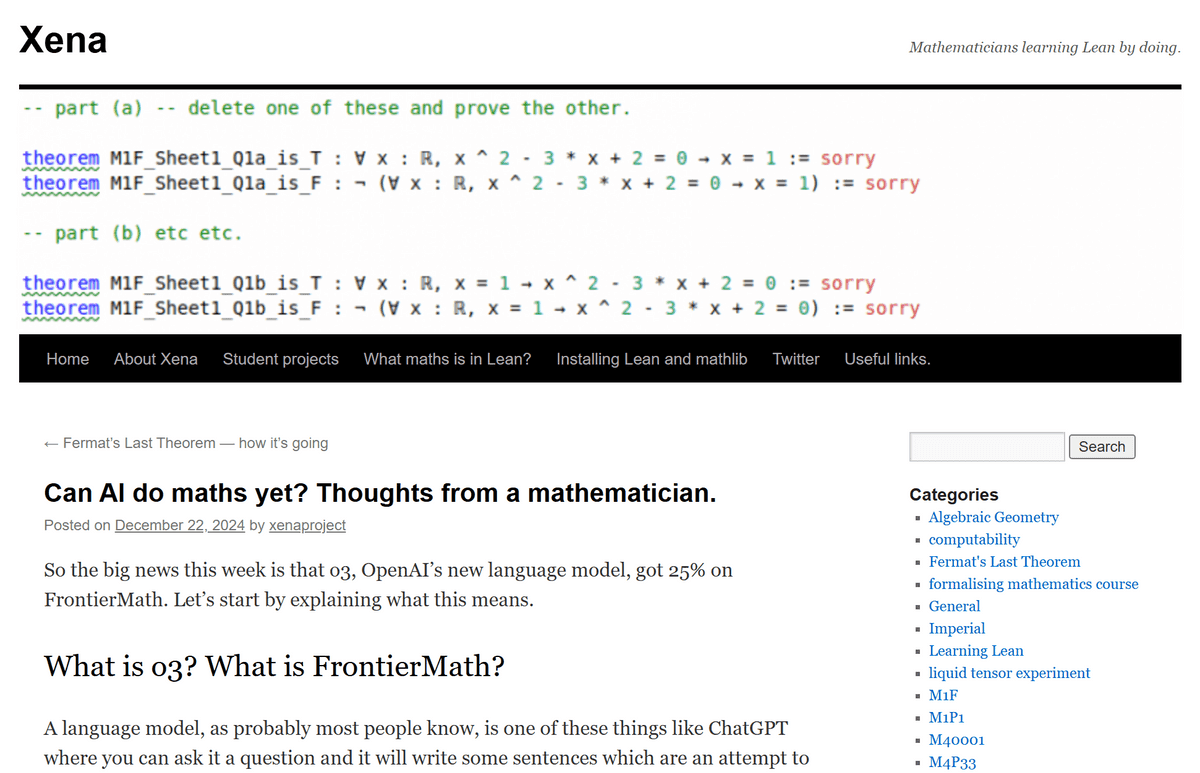
It has been revealed that the o3 model achieved a score of 25.2% on the FrontierMath problem dataset. FrontierMath is a dataset of hundreds of difficult mathematical problems, and not only the problems themselves but also the number of problems in the entire dataset are kept secret, and the AI is carefully designed not to train problems in advance.

All problems in FrontierMath are calculation problems, and do not include problems in the form of 'prove it'. The answers to the five sample problems published are all positive integers, and the other problems are said to have 'clear and computable answers that can be automatically verified'. The difficulty of the problems is quite high, and even mathematician Buzzard was only able to solve two of the sample problems, and although he thought that he could solve another problem if he tried, he thought that he could not solve the remaining two problems.

The FrontierMath paper includes difficulty ratings from well-known mathematicians, including Fields Medal winners, who comment that the problems are 'extremely difficult,' suggesting that only experts in the field of each problem could solve them. In fact, the two problems that Buzzard was able to solve were in his field of expertise.

In addition, since real mathematicians spend most of their time on proofs and coming up with ideas for proofs, rather than on calculations, some mathematicians argue that 'calculating to get a numerical answer is completely different from coming up with an original proof,' making it unsuitable for measuring mathematical ability. However, since grading proofs is costly, the model uses calculation problems that can be graded simply by checking whether the answer submitted by the model matches the correct answer.

Buzzard said he was 'shocked' that OpenAI's o3 model scored 25.2% on the FrontierMath test.

It has been shown that AI is good at solving 'Mathematical Olympiad-style' problems that excellent high school students solve, and Buzzard had no doubt that AI would be able to solve university undergraduate level mathematics problems, which are similar in that 'there are many typical problems. However, Buzzard commented that 'it seems like a pretty big leap has been made' in that AI has acquired a level of mathematical ability that goes beyond the level of typical problems and can respond with innovative ideas to problems at the early level of doctoral programs.

However, Elliot Glaser of Epoch AI, who built FrontierMath, said that 25% of the problems in the dataset are in the format of the Mathematical Olympiad. Since all five sample problems published are completely different from the format of the Mathematical Olympiad, Buzzard was very excited to hear that the o3 model scored 25.2% on FrontierMath, but his excitement subsided when he found out that 25% were in the Mathematical Olympiad format. 'I look forward to seeing AI score 50% on FrontierMath in the future,' Buzzard commented.


Currently, AI is making rapid progress, but there is still a long way to go and a lot of work to be done. Buzzard concluded his blog by saying that he hopes that AI will eventually acquire the mathematical skills to handle problems at the level of 'prove this theorem correctly and explain why the proof works in a way that humans can understand.'