Is the reason for the large number of math geniuses in the former Soviet Union due to early childhood 'math club' education?

The countries that made up the Soviet Union, which collapsed in 1991, have produced many talented people. In particular, critic John Smith, based on the writings of mathematician Alexander Zvonkin, points out the existence of 'math circles' as a reason for the emergence of so many mathematical geniuses.
REVIEW: Math from Three to Seven, by Alexander Zvonkin

Math circles are informal groups of people who really enjoy math and want to spend time thinking and talking about it. They are similar to sports teams in that they foster friendships with their own internal culture and often have a particularly talented 'coach,' but they differ in that they cooperate rather than compete with each other. Math circles originated in the pre-revolutionary Russian Empire and then spread throughout the Soviet Union.
The problems we work on in math clubs are very different from the math we learn at school. School math consists mostly of educational exercises, but in math clubs we work on interesting questions that come up when someone is actually trying to do something. These are problems that may or may not have an answer, and even if they do, it may only come after months of dedicated work.
In the math club, the coach sometimes chooses problems to help each member improve their skills, and sometimes the whole club works together to solve problems that no one knows the answer to. Even the best members of the club push themselves to their limits and still can't find the answer to some difficult problems, but such 'defeats' are only possible because they chose the right opponent, and even if they lose once, they often try again.
Smith shares the story of Alexander Zvonkin, a professional mathematician who decided to hold a math club for a group of three- and four-year-old children in his neighborhood.
It's hard enough to get a three-year-old to sit still, but even harder to get them to do math. Zvonkin wrote in his diary about the struggles he faced, such as 'I had a great idea for a puzzle, but everyone started yelling and it got out of hand.' In the first year, the kids weren't ready to tackle problems, so Zvonkin focused on 'reverse programming' their schoolwork.
Zvonkin hates the way schools reduce math to a 'series of formulas' and despises teachers who subtract points for slightly different answer formats, calling them 'stupid.' The worst part is when teachers subtract points when students use 'techniques they shouldn't know about yet.' During the first year of the math group, Zvonkin taught the kids not to blindly believe in school-based education.
A year later, Zvonkin gave the children their first problem: 'If you have to choose two out of five objects, how many ways can you choose them, regardless of the order in which you choose them?' Because the children were still four years old and not yet capable of formal, symbolic reasoning, Zvonkin used red and blue beads to help them visually tackle the problem.

Even after working on the same problem over and over for several months, 4-year-olds are still far from understanding how to count the number of choices when choosing k items from n items. Zvonkin worked on other problems for a while to fade the children's memories of the story of how to choose, and then tried to recall their memories by asking similar questions such as 'How many combinations are there when coloring only two of five circular pieces of paper?' and 'How many ways to choose a path from the bottom left to the top right on a 4x3 map?'
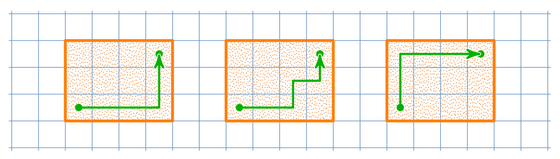
The 4-year-olds had a hard time realizing that it was the same problem on their own, but when Zvonkin put a red mark on the right when choosing a path and a blue mark on the up, the children realized that it was the same problem and made a big fuss. However, the children still haven't been able to find the answer.
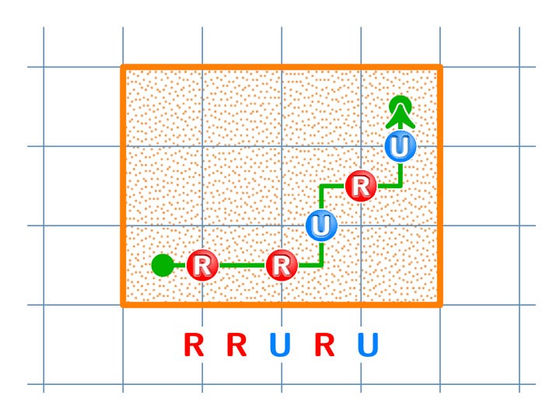
After waiting a few months, Zvonkin again asked the children to guess how many combinations they could put two balls into five empty boxes. This time, the children immediately realized that it was the same as the bead puzzle. This realization showed that they were ready to tackle the problem head on.
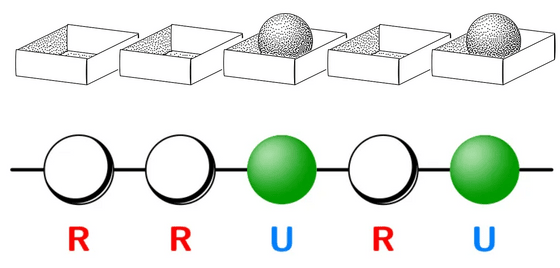
Thus, through four years of circle activities, Mr. Zvonkin succeeded in teaching mathematics to his son and other children of the same age in the neighborhood, despite the difficulties. Mr. Zvonkin kept a detailed diary, and tried to try a second circle activity using the knowledge of 'what went well and what didn't' from the diary, but the knowledge from the first circle was not useful for the second circle, and mathematics was not taught well, so it was disbanded after one year.
As any parent who has raised multiple children knows, even if they are raised in the same way, each child will show their own unique personality. Smith defended Zvonkin's failure, saying, 'Children are not blank slates that can be programmed, but aliens that create new universes.'
Zvonkin's diary has been published under the title 'Math from Three to Seven' and is available to purchase on Amazon.
Amazon.co.jp: Math from Three to Seven: The Story of a Mathematical Circle for Preschoolers (MSRI Mathematical Circles Library Book 5) (English Edition) eBook: Zvonkin, Alexander: Kindle Store
Related Posts:
in Free Member, Education, Note, Posted by log1d_ts







