A video showing how miraculous the probability of 'shikanokokonokoshitantan' appearing in a Markov chain is

The TV anime '
[Markov chain] Shikanoko but it's a Markov chain - YouTube
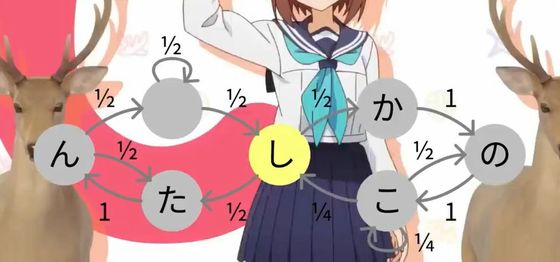
A Markov chain is a sequence of random variables that satisfies P(X t+1 ∣X t ,X t−1 ,…,X 1 )=P(X t+1 ∣X t ). Simply put, it is a sequence in which X t+1 depends only on X t and appears before X t−1 without any relation.
Applying this to 'shikanokokonokokoshitantan,' there are two possibilities for the character following 'shi,' 'shi → ka' or 'shi → ta,' with a probability of 1/2 for each. The only character following 'ka' is 'ka → no,' with a probability of 1. The only character following 'ta' is 'ta → n,' with a probability of 1. The only character following 'no' is 'no → ko,' with a probability of 1. The character following 'n' is 'n → ta' or 'n → ○ (end of the string),' with a probability of 1/2 for each. The characters following 'ko' are 'ko → no,' with a probability of 1/2, 'ko → ko,' with a probability of 1/4, and 'ko → shi,' with a probability of 1/4.
It's a bit complicated to write down, but here's a diagram: In the video, we generate a Markov chain sequence according to this rule, and watch to see if 'shikanokokonokokoshitantan' appears.
If you consider the time it takes to reach the end of the line as one phrase, the first phrase in the video is 'shikanokokokoshitan.' I feel like that's a bit of a shame.

Next is 'Shikanokoshitan'
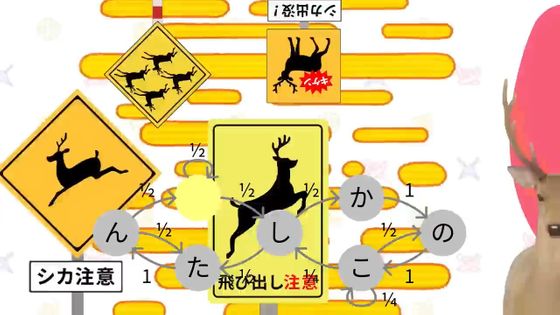
Next came 'shikanokokokokokokokokokoshikanokokokokokoshikanokokokokokokoshitantantan.' Although it was a possible pattern, the phrase was far too long.

Then, the next phrase ends with the shortest possible 'shitan.' There are only six possible characters: 'shi,' 'ka,' 'no,' 'ko,' 'ta,' and 'n.' Even though the next character is heavily restricted by the previous character, you can see that there are a considerable number of possible patterns.

If you listen carefully, you'll come across parts where the same phrase is repeated.

The phrase that begins


As I continued watching the video, I began to understand just how miraculous the probability of 'Shikanokokonokokoshitantan' appearing is, and I felt like I would be moved every time I watched the opening from now on.
According to the video uploader, 'If the current state is 'shi', the probability that it is the beginning of 'shikanokokonokoshitantan' is 1/512.' Taking into account stationary probability and frame length, it seems that 'shikanokokonokoshitantan' will appear about once every 11 minutes.
If you want to listen to the original 'Shika no Konoko Koko Shitantan' from 'Shikairo Days', you can check it out in the 'Shika no Konoko Koko Shitantan' non-credit OP video released below. The number of views of the non-credit OP video has reached about 16.5 million at the time of writing.
TV anime 'Shika no Kokono Kokoshitantan' non-credit opening video 'Shika-iro Days' - YouTube
◆ Forum is currently open
A forum related to this article has been set up on the official GIGAZINE Discord server . Anyone can post freely, so please feel free to comment! If you do not have a Discord account, please refer to the account creation procedure article to create an account!
• Discord | 'Did you watch 'Shikanokokonokokoshitantan'? Was it interesting?' | GIGAZINE
https://discord.com/channels/1037961069903216680/1264874972795633746
Related Posts: