What is 'exponential smoothing,' a technique for making animations look smooth?

Graphics developer Nikita Lisitsa has posted a post explaining his favorite technique, exponential smoothing, which he says he uses 'everywhere in his products.'
My favourite animation trick: exponential smoothing | lisyarus blog
https://lisyarus.github.io/blog/programming/2023/02/21/exponential-smoothing.html
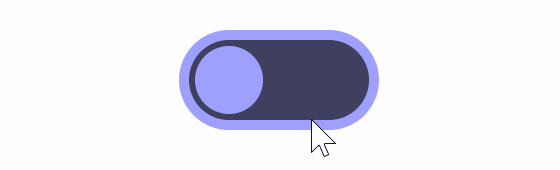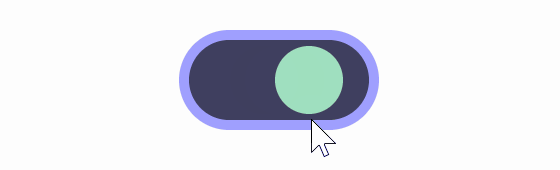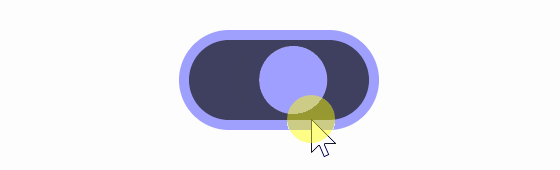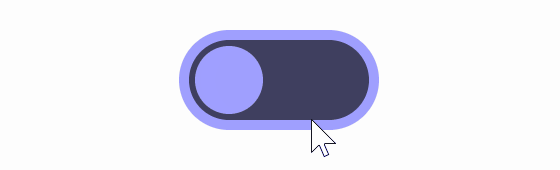
Lisitsa uses the example of a toggle button, as shown below. Clicking it switches between 'on' and 'off.' There are no animations set up yet, and the toggle button simply moves between the left and right edges.
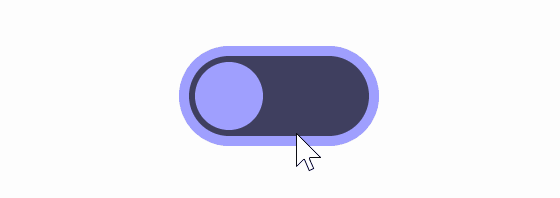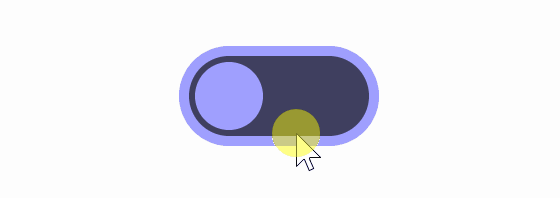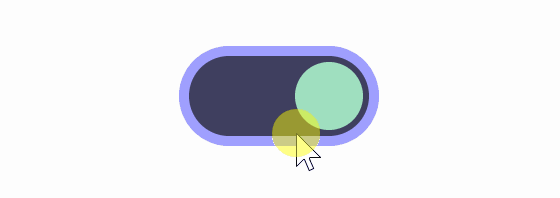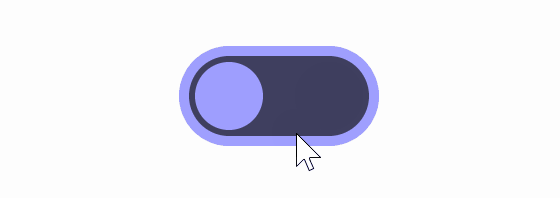
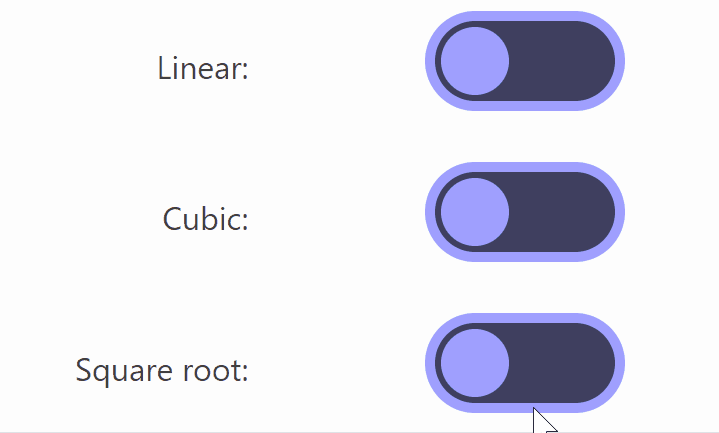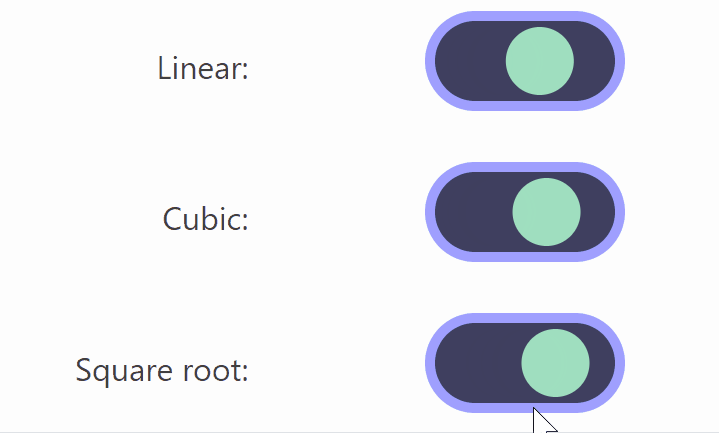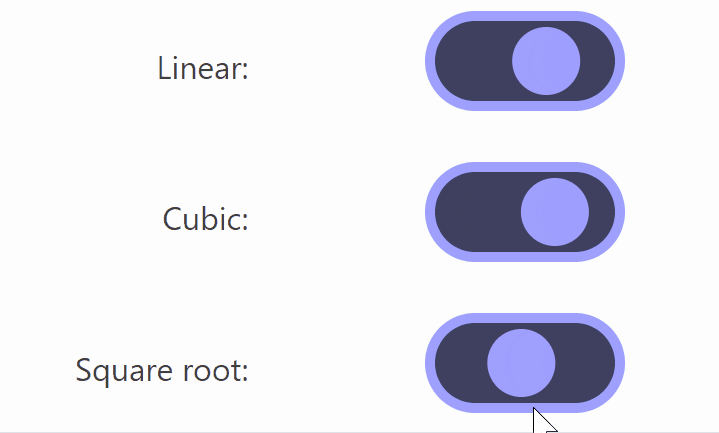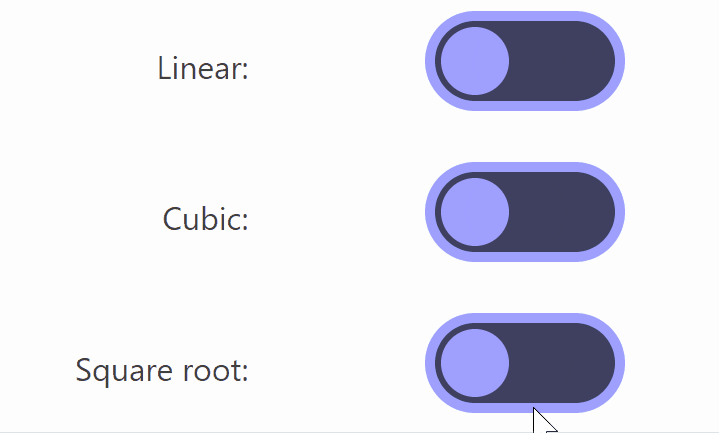
Functionally, there is no problem even if animation is not set, but adding animation makes it easier for users to understand what is happening. If you set an animation that moves the button at a constant speed, it will look like the image below.
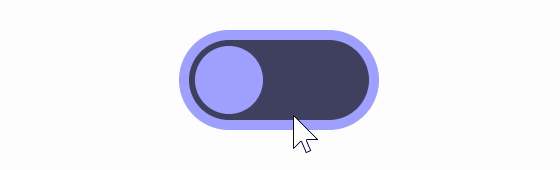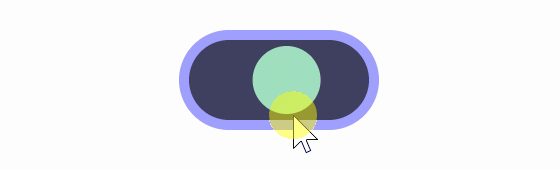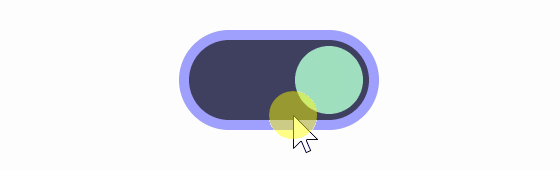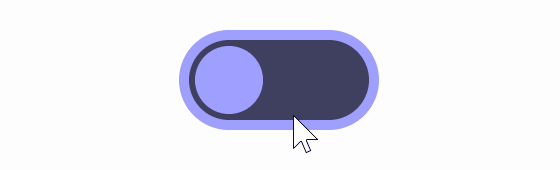
A constant animation speed can look a bit choppy, so if you change the speed to a classic Bezier curve , '3t^2-2t^3', you get the result below.
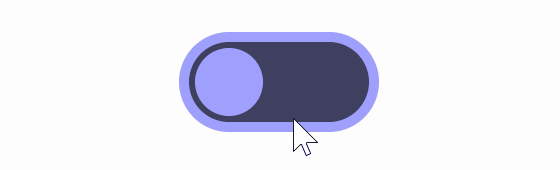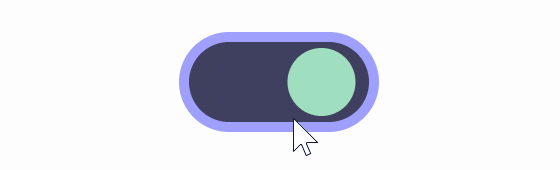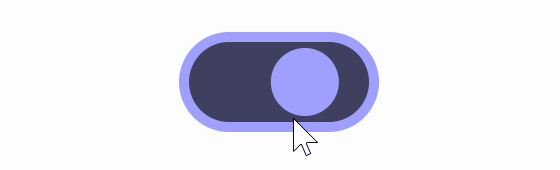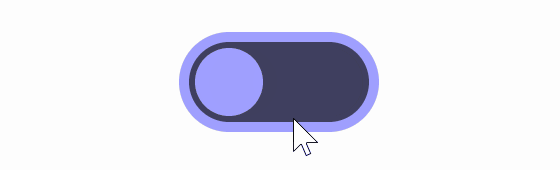
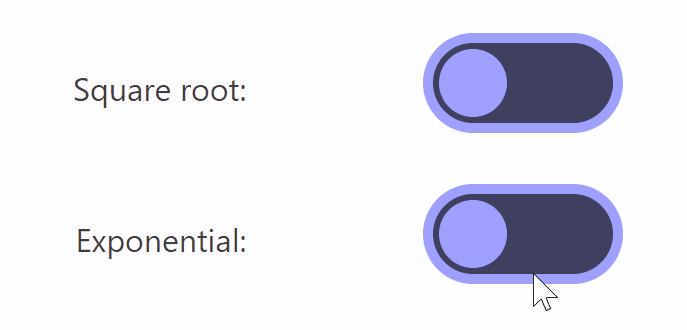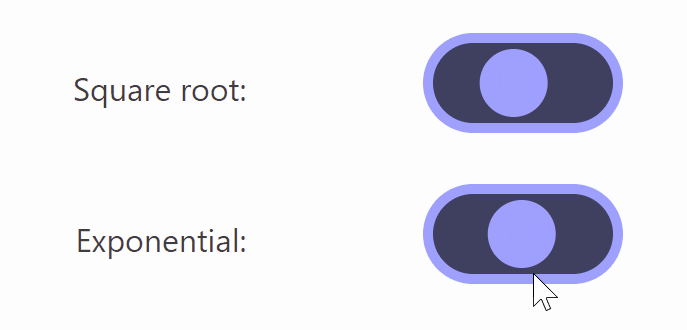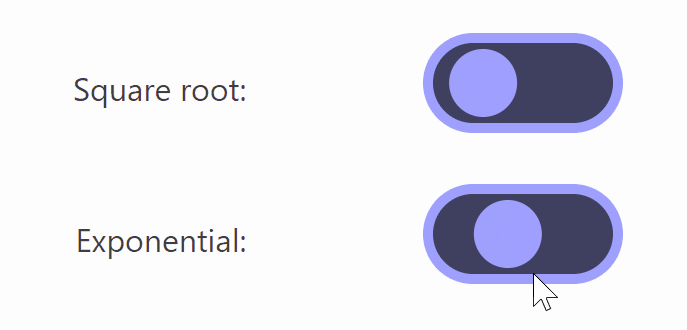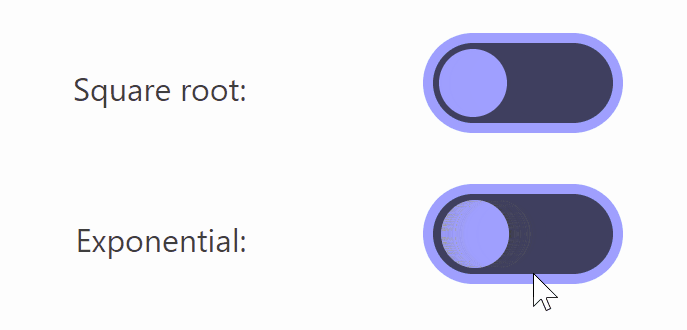
Also, if you change it to “sqrt(t)” using the square root, you get the result shown below.
The differences between the three above are difficult to notice, but when you slow down the footage, the differences become clear, as shown in the image below.
Of these, Lisitsa said he likes animations using square roots the most because 'the movement starts large and slows down as it approaches the destination.' However, when using square roots, the animation when switching from 'off' to 'on' is 'sqrt(t)', but to achieve the same movement on the opposite side of 'on' to 'off', the formula '1-sqrt(1-t)' is required, which causes the button to warp when switching on and off in the middle of the animation.
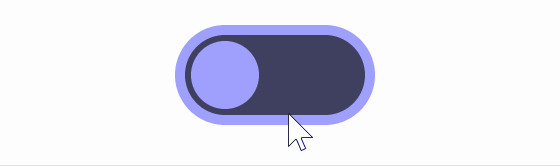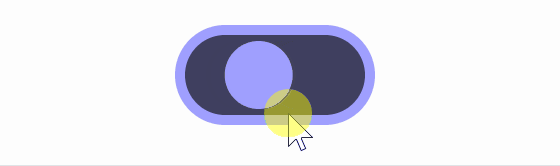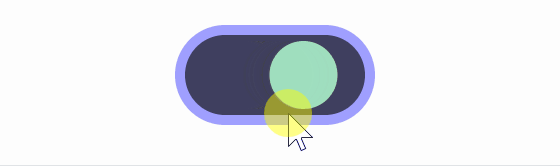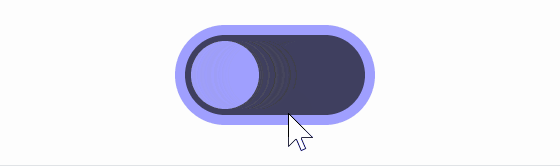
The formula for animation developed by Lisitsa to take advantage of the advantages of square root animation while minimizing warping is 'position.x += (target - position.x)*(1-exp(-dt*speed))'. Lisitsa named animation using this formula exponential smoothing.
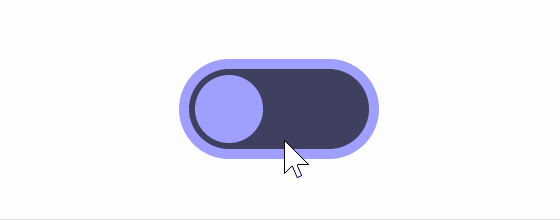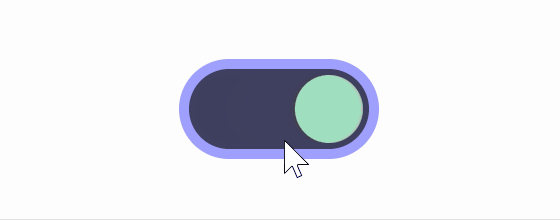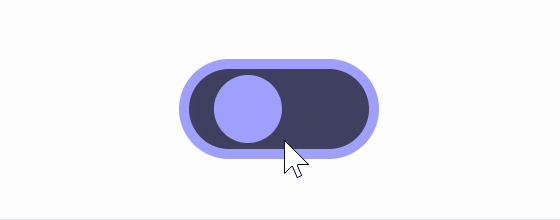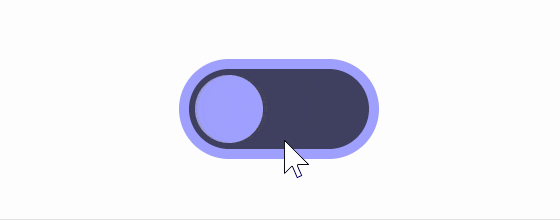
The comparison with the square root is shown in the figure below. You can see that the button barely warps even when switched on and off midway.
The amount of change in position in exponential smoothing, '(1-exp(-dt*speed))', may look strange at first glance, but it is actually a formula derived by solving the differential equation below, where the current position is x, the target position is a, and the speed is c. The original blog has detailed calculations, so if you're interested, check it out.
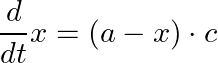
Related Posts:
in Note, Posted by log1d_ts