Mar 22, 2020 16:00:00

What is the 'shape of the universe' as seen from the angle of the triangle?

Although it is an open fact that the earth is round, no conclusion has been reached on the shape of the universe even in 2020, and it is still a major theme. Erica Claraiich, a journalist specializing in mathematics and science, explains what the shape of the universe is specifically thought of from the viewpoint of 'angle of triangle'.

What Is the Geometry of the Universe? | Quanta Magazine
https://www.quantamagazine.org/what-is-the-geometry-of-the-universe-20200316/

◆ The theory that the universe is flat
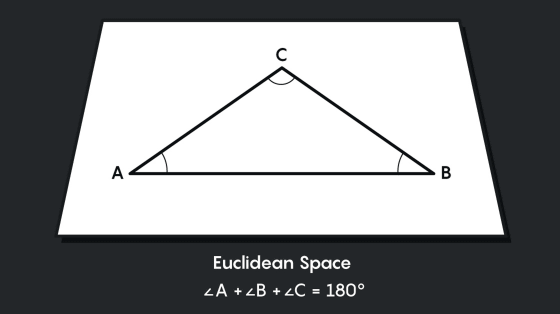
One hypothesis about the shape of the universe is that the universe is in the space of Euclidean geometry and flat. In Euclidean geometry, it is assumed that straight lines extend everywhere, planes are flat everywhere, and parallel lines are parallel without intersecting. In this space, the triangles are drawn as straight lines, so the sum of the angles is 180 degrees.

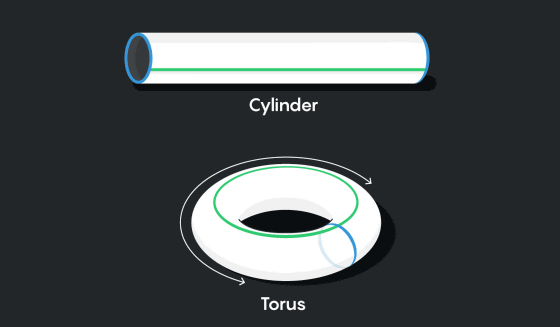
It is difficult to visualize a flat universe, and it is easier to understand by capturing from a two-dimensional space instead of a three-dimensional space. First, imagine a rectangular plane, and then attach the top and bottom edges to form a cylinder.

Next, attach the ends of the cylinder to create a donut-shaped

torus .

Then, inside the torus, imagine three types of lines that loop back to the starting position. One is a line parallel to the long side of the rectangle, one is a line parallel to the short side of the rectangle, and the other is a straight line connecting the diagonals of the rectangle.

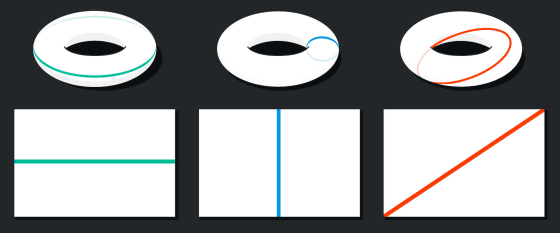
The three types of lines appear to be curved on the torus, but they are straight lines when viewed on a plane. The light also travels along a straight line in the torus, so if a person standing inside the torus looks straight at the direction of light, he can see himself from the back.

In other words, inside the torus, there are loops of light in various directions that allow you to see yourself from behind.

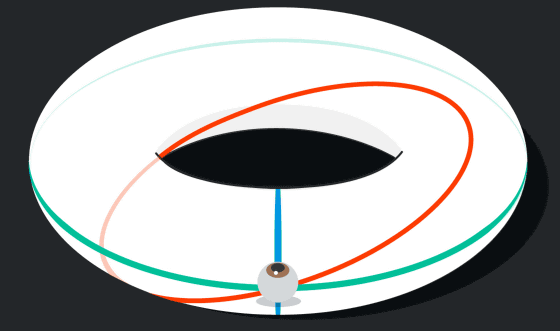
When you return the situation in the torus to a plane, for example, the light that travels from the front to the back of yourself repeats a loop that returns to the front again when it reaches the back.

If you compare a plane to a room, a loop of light that travels from front to back creates the appearance of a room and your image before and after you. A myriad of rooms and statues can be seen through loops of light in different directions returning from you, not just from the front to the back.

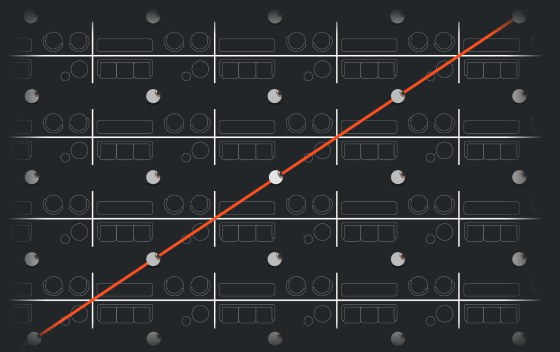
Strictly speaking, the universe is not a plane, but a torus with a series of rectangular boxes. You can't visualize this space, but you can imagine the creatures in it.

When one plane is compared to a room, the humans in the three-dimensional torus are infinitely cuboid, as if the humans in the plane torus lived in the same infinite rectangular room. You live in a room and you see endless copies of yourself in every direction.

For this reason, from the human eye's perspective, the universe should look like an infinite series of the same things, but if you look at the real universe, you cannot see an infinite copy of yourself. Because the universe is vast and it takes a tremendous amount of time for the same light to reach humans.

So, to prove that the universe is flat, astronomers do not look for light to see their own copy in the universe, but rather the furthest that can be seen in the universe, i.e. immediately after the Big Bang For the continuum of

Cosmic Microwave Background Radiation (CMB) left in Japan.

In other words, this means searching for a CMB in which an abnormally high temperature red area (hot spot) and an abnormally low temperature blue area (cold spot) have the same pattern in the temperature distribution image map. When the same pattern of CMB is found in two different directions, it suggests that the universe is flat.

◆ Theory that the universe is spherical
Measuring triangles in space is one of the important ways astronomers test whether the universe is bent. If we consider that the shape of the universe is spherical, that is, a spherical shape similar to the earth, unlike a flat universe, the shape of the universe is calculated by adding the corners of the triangle from the points of the universe detected by the measurement. Can be proved.

In spherical geometry, straight lines describe great circles, triangles have a bulging shape, and the sum of the three corners is more than 180 degrees.

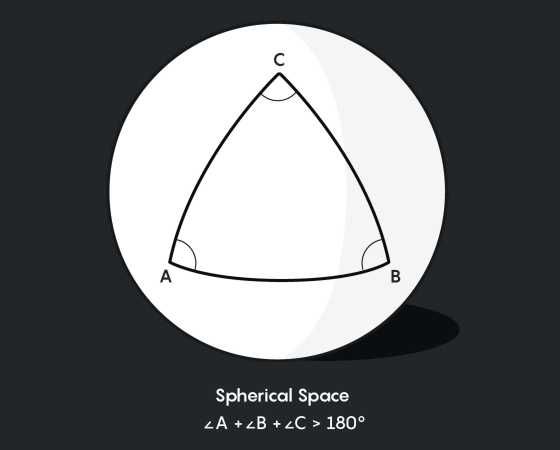
In spherical geometry, a straight line is a great circle, so the great circle connecting the hot spot or cold spot in the CMB is measured as a straight line. From the great circle, measure the triangle with reference to the position of the earth, and calculate from the length and angle of the sides of the triangle whether the sum of the angles of the triangle is 180 degrees or more.

In a 2018

study , some of the data obtained from satellite plank claimed that `` the universe is spherical '', but other researchers have argued that it is `` a statistical error '' You.

◆ Theory that the universe is a hyperbolic plane
The figure below shows a hyperbolic plane called the Poincare disk . There is a theory that the universe spreads like a Poincare disk.

In a plan view, the outer triangles appear smaller, but from a

hyperbolic geometry perspective, all triangles are considered to be the same size. The boundaries of the circle extend infinitely in all directions, and the number of triangles near the boundary grows exponentially.

Also, in hyperbolic geometry, the sum of the angles of the triangles is less than 180 degrees. For example, the sum of the angles of the triangles on the Poincare disk below is 30 degrees + 90 degrees + 45 degrees = 165 degrees.

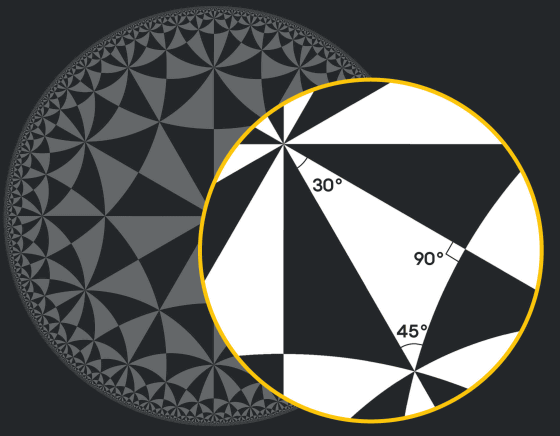
The sides of these triangles do not look straight, but because they forcibly represent hyperbolic geometry on a plane, they appear to be through a distorted lens, so they live on the Poincare disk. For some living creatures, this curve looks straight, and the shortest route from A to B is:

At the time of writing, the theory that the universe is flat is supported. But Klareich says, 'We cannot deny the possibility of being either spherical or hyperbolic.' This is because the universe is vast, and the total angle of triangles in spherical or hyperbolic geometry is said to be very small compared to the total angle of triangles in a plane universe.

`` If the universe is a very large sphere or hyperbolic shape, the part that can be observed with modern technology is almost flat, and the curvature is ultra-precise as human beings have not invented yet It can only be detected with a unique device. '