The waiting time of customers can be dramatically shortened simply by increasing the number of events reception / cashier / window teller etc from 1 person to 2 persons

" Queuing theory " is the theory aimed at analyzing scenes that customers queue in order to receive services using mathematical models. This queuing theory is applicable not only to windows and cash registers where people are lined up but also to any system with clients and servers. According to such queuing theory, it is said that waiting time on the queue side is dramatically eliminated simply by increasing the number of events acceptance, cashier in charge, bank counters etc from one to two.

What happens when you add a new teller?
https://www.johndcook.com/blog/2008/10/21/what-happens-when-you-add-a-new-teller/

Server utilization: Joel on queuing
https://www.johndcook.com/blog/2009/01/30/server-utilization-joel-on-queuing/

Dr. John D. Cook, who works as a data consultant, explains the usefulness of queuing theory. Dr. Cook explains how the standby queue decreases just by increasing the number of contact persons by one as an example, "When there is only one window teller in a small bank".

Assuming that the time taken for a customer to receive service at the bank's window is "average 10 minutes" and the number of visitors per hour is "5.8 people", the waiting time for people queuing in order to receive service is How long will it be?

Assuming that "the timing the customer arrives at the bank" and "the time taken for the customer to receive the service" are random, if there is only one teller to serve, the time the customer waits in line to receive service The average of "what about 5 hours " will be. However, increasing the window teller to two people dramatically reduces the average waiting time to " about 3 minutes " rather than half. Simple calculation, it seems that queue waiting time can be shortened by 93 times just by setting two windows.

As customers interact with tellers for an average of 10 minutes and the customer has an average pace of 10.3 minutes to the bank, if the customer's pace of visit is constant and the response time ends up perfectly 10 minutes each time, can not. However, in reality, there are cases where two customers visit in 10 minutes, customers do not visit for 30 minutes, cases where it takes 20 minutes for one person to respond, and cases where it takes only 5 minutes, In the case of a bank like this, a standby queue of " average 28 people " will be formed in front of the window. This is used as a typical example in queuing theory, and by using Poisson distribution , the waiting time per customer is calculated.

The method of calculating the waiting time in the matrix is summarized in the following page considerably easily, so please check it if you are interested.

- Queues that can be seen by monkeys

Of particular importance in queuing theory is the rate of change of "customer visit pace (5.8 people per hour in the above example)" and "time spent on service delivery (average 10 minutes in the above example) is. While the visit pace and service provision time are moving averaged according to the average value, the number of matrices is minimal, but if they vary, that is, when the volatility rate is high, a long standby queue is formed at once.

This queuing theory can be applied to not only cases where people actually form a row such as event reception / cashier / window teller but also to any system equipped with client and server. The following graph is a visually easy-to-understand representation of how the waiting time of the server changes using queuing theory. The vertical axis shows the standby time of the server, and the horizontal axis shows the utilization rate. It should be understood that as the utilization rate increases the standby time jumps exponentially.

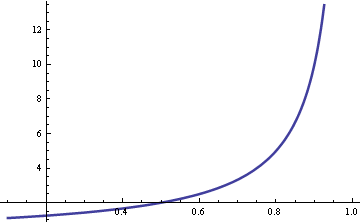
If you add one server just like adding one window to the bank here, it will be possible to dramatically shorten the waiting time that was too long on one server.