Mathematician invented 'How to cut pizza equally and easily'

When cutting for pizza sharing by several people, usually cut it by straight lines passing through the center of pizza several times and cut it into 4, 6, 8 pieces. However, with this method one piece becomes thinner as the number of people increases, and as soon as the number increases too much, you must eat pizza like pimples. In order to solve such inconvenience, a mathematician invented "a method of cutting pizza where everyone can eat pieces that are equally easy to eat".

Mathematicians invent new way to slice pizza into exotic shapes | New Scientist
https://www.newscientist.com/article/dn28743-mathematicians-invent-new-way-to-slice-pizza-into-exotic-shapes/

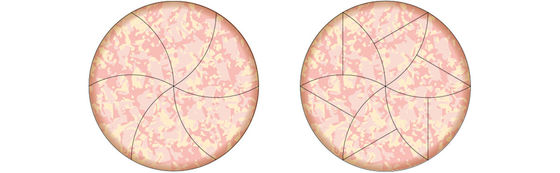
From the past, "a method to divide the pizza into 12 equal pieces" was known. In this way, first draw three lines that intersect at the center point, drawing a gentle curve and traversing from end to end of the pizza. With this, six equally divided pieces that are curved and bent are completed. Next, cut from the point where the outer circumference and the cut line intersects with a line extending from the center to the center point of the line extending from the center to the outer periphery. As a result, "12 pieces of the same shape and the same size" is completed as a reason.

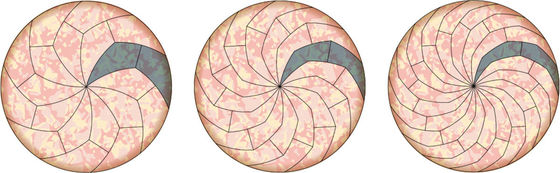
Mr. Joel Hadley who is studying mathematics at the University of Liverpool and Mr. Stephen Wassy mathematically invented a method to further generalize "How to divide the pizza into twelve equal parts" and to create even more equally divided pieces Did. First of all like a method to divide a pizza into 12 equal parts, we will create a piece that curves outward from the center. At that time, the point is to make the piece an odd polygon like a pentagon, a heptagon, a nigagon ......

Next, if you cut the polygon piece just in the middle, you can mass produce pieces of the same size and shape. "Mathematically, no matter how many corners of a polygon you can increase, you can produce as many pieces of pizza as you can," Hadley said, but in fact it is impossible to cut pizza with this technique with tremendous skill and There is no doubt that patience will be needed. In reality, it is difficult to cut the first piece beyond the octagon.

Also, in this cutting method, it is divided into a piece with a pizza ear part and a piece without an ear part. A conflict may occur a little if the percentage of people like "I want to eat the pizza's ears part" or "I do not want to eat pizza's ears as much as possible" is biased toward either.

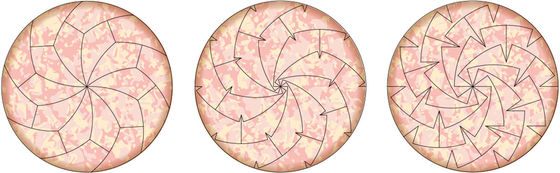
In addition, they proved that adding a slit when cutting a pizza can also produce a more complex piece. When coming so far it will become an atmosphere that cuts for mathematical pleasure rather than cutting pizza to eat any longer.

Unfortunately even having Mr. Hadley and Mr. Worthy's brain, the possibility that the two people discovered the "polygon theorem of pizza-cut" for applications other than pizza cut is unlikely to be found for a while. Mr. Hadley said, "I do not know if I can apply the cutting method I found this time to work other than cutting pizza, but I can take pictures of nice pizzas that are at least mathematically interesting," It is.

by Joel Haddley