Physicist creates the world's most brutal maze

British and Swiss physicists have published the results of their research into how to generate terrifyingly difficult mazes, a discovery that could have applications in nanotechnology and biotechnology.
Physical Review X - Accepted Paper: Hamiltonian cycles on Ammann-Beenker Tilings
Physicists Have Created The World's Most Fiendishly Difficult Maze: ScienceAlert
https://www.sciencealert.com/physicists-have-created-the-worlds-most-fiendishly-difficult-maze
In this study, a research team led by theoretical physicist Felix Fricker of the University of Bristol in the UK was inspired by fractal geometry and the mathematical puzzle ' Knight's Tour ,' which explores how chess pieces move, to derive an algorithm that explains the patterns of a material called a quasicrystal, which is rarely seen in nature.
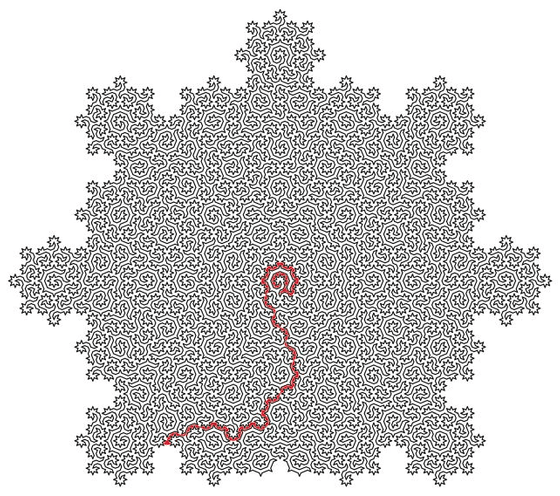
Below is an example of such a maze. We will explain how to escape the maze later.

The knight tour is a unique way to visit every square on a chessboard using a knight piece that can jump to the left or right of two squares in front or behind. This is also a type of
Fricker and his colleagues believe that studying Hamiltonian circuits in quasicrystals, which lack translational symmetry - that is, the property that they can be superimposed by moving certain parts in parallel - could help us understand the structure of materials.
The research team then generated the aforementioned maze by generating a Hamiltonian circuit on a two-dimensional pattern of Amman-Baker tiles , a typical structure of quasicrystals.
This thick line is Aman Baker tile.

The resulting circuit passes through each atom of the quasicrystal once, connecting all the atoms in a single line without overlapping, and can be infinitely expanded or contracted, exhibiting a fractal structure in which the smallest parts resemble larger parts.
Drawing a maze with a start and an exit using these lines can be a fun way to kill time, but the theory behind identifying Hamiltonian loops in quasicrystal structures could also be used to solve the traveling salesman problem and find the optimal way to analyze the structure of quasicrystals using
'Our study shows that quasicrystals have the potential to have better adsorption properties than crystals,' said Shobna Singh of the University of Bristol, co-author of the paper. 'For example, flexible molecules are more likely to adhere to the disordered quasicrystals than to the ordered atomic structures of crystals, and because quasicrystals are brittle and can be easily broken down into small particles, it could be easy to increase the surface area for adsorption.'
An example answer to the maze mentioned above looks like this:
Related Posts:
in Science, Posted by log1l_ks