Summary of 'effective spaced repetition' methods that are useful for efficient learning and study

by
It is said that for effective learning, it is important to study the same content repeatedly at intervals. Programmer Fernando Boretti introduces the method of 'spaced repetition' necessary for effective learning.
Effective Spaced Repetition
https://borretti.me/article/effective-spaced-repetition

◆What is spaced repetition?
First, create a flashcard with a question on the front and the answer on the back. Periodically look at the card to recall the answer and turn it over to check. If you have memorized it correctly, you will remember the answer even if the interval between looking at the card is long. It is recommended to use a vocabulary book or software such as
Factors that limit spaced repetition
There are two factors that limit spaced repetition: difficulty in forming a habit and writing effective flashcards. Boretti tested flashcards as part of his daily routine every morning, but some people find this difficult to do. So, if Boretti didn't tackle the flashcards, he used an app that left them for the next day.
Creating effective flashcards was a skill that took Boretti a while to master. Many of the cards he created in the first few months were insufficient to be retained in long-term memory . It takes time and trial and error to develop effective flashcards.
Words of encouragement
Learning is an automatic, instinctive process, but traditional schooling has taught us that the idea of learning arouses our aversion. Boretti points out that you don't need to be particularly smart or averse to learn effectively.
◆ Rules for learning
Boretti outlines his own rules for effective spaced repetition:
First, understand
Before creating flashcards, you need to make sure the information is clear in your head. Boretti digs into the text until he has a good understanding of the subject, and then he starts creating flashcards.
・Be honest
If you remember something incorrectly during a flashcard test, it's important to acknowledge it and say, 'I forgot,' rather than making excuses.
・Have fun
If you're reluctant to use flashcard tests, you'll have trouble maintaining the habit. Boretti suggests using different testing software and creating short, concise flashcards.

by
Repeat as many times as you like
Individual flashcards should be short and concise, but it's important to test the entire deck of flashcards as many times as you like until you have them memorized.
・Organize by source
Different sources often organize knowledge differently, so it's important to organize your content by source rather than by topic. Rather than creating a perfect organizational structure, create a deck for each source and sub-decks for each piece of content, so you can easily keep track of your progress through the text.
Create concise flashcards
When creating flash cards, keep them short and concise. If the cards are complicated and long, they will be hard to remember and difficult to grade objectively.
Write two-way questions
A good rule of thumb is to write flashcard questions in two ways, 'term to definition' and 'definition to term,' as much as possible. This helps students understand and retain information about a particular concept.
Ask questions in multiple ways
It's important to ask questions in multiple ways, including formal and informal definitions and theorem statements, contextual questions, and questions that connect different concepts. 'The ultimate goal is to have as interlinked a knowledge graph as possible,' Boretti says.
・Creating a conceptual diagram
Creating a concept map helps you visualize the concepts you are acquiring in a graphical way.
・Hierarchical learning
Many concepts can be classified hierarchically, linked by superclass-subclass relationships. To reinforce this hierarchy, we encourage you to ask questions like 'What is a subclass of ____?' and '____ is a subclass of what?'

by
・Learning sequence
When studying a sequence of information, it is important to create test cards that require you to recite the information from start to finish, close sequence cards that require you to fill in the blanks for each piece of information, cards that provide context and ask you to fill in the blanks, etc. The type and number of flash cards you use will depend on the nature of the information you are studying.
◆ Learning examples
Boretti gives the example of learning using flashcards.
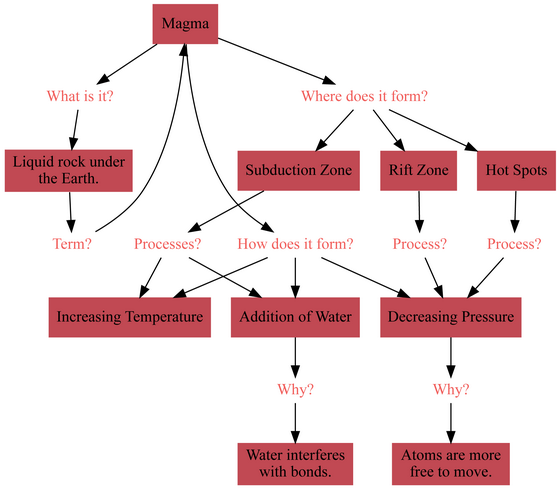
-Magma formation
To learn about magma formation in geology, we organize the information into three broad categories: 'Definition of magma,' 'How magma is formed,' and 'Where magma is formed.' For each category, we break down the information hierarchically and create flashcards with questions such as lists, details, explanations, cause, and effect. The flashcards we created include questions such as 'What is magma?', 'What is the process by which magma is formed?', and 'How is magma formed at hotspots ?', and are designed to make memorization easy.
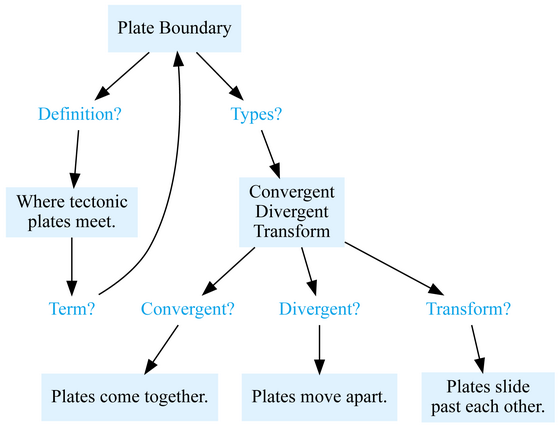
・Plate tectonics
The Plate Tectonics example demonstrates creating interactive flashcards that focus on the concept of plate boundaries and different boundary types such as convergent boundaries, divergent boundaries , and transform faults . For the term 'plate boundary,' the example demonstrates creating two flashcards that include both a definition and the corresponding term.
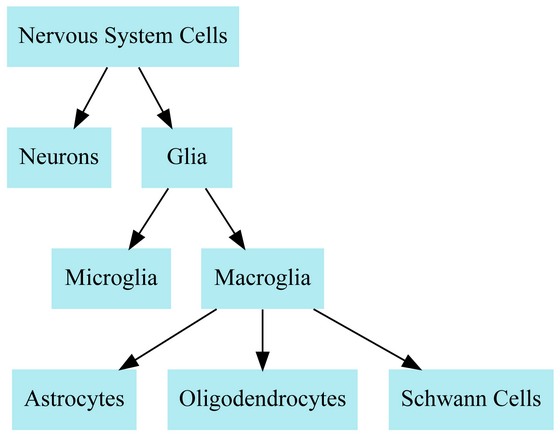
-Nerve cells
In the example of nerve cells, the types of cells in the nervous system are divided into
Types of neurons
When learning about neuron types, creating separate flashcards for the functional classification of
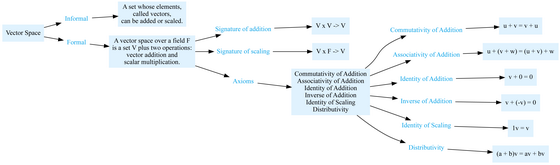
・Vector space
The axioms that define vector spaces , which are sets of elements called ' vectors ' that can be added and contracted, include 'commutativity of addition,' 'associativity of addition,' 'identity of addition,' 'reciprocal of addition,' 'identity of scaling,' and 'distributivity.' It is important to break down these axioms and learn their meaning step by step.
・Even-oddity
Odd-even is a group that describes the rules for adding even and odd numbers. The table below shows the configuration of even and odd numbers that make up odd-even.
| + | even number | odd number |
| even number | even number | odd number |
| odd number | odd number | even number |
Students are expected to convert the table above into flashcards and create questions. For example, if the front side asks 'What is an even-odd set?', the answer on the back would be 'It is a set that represents the rules for adding even and odd numbers,' and if the back side asks 'Even number + even number =?', the answer would be 'Even number.'
Logical conclusion
Logical consequence has two concepts: 'semantic consequence' and 'syntactic consequence.' Semantic consequence is defined as 'if for every concept for which concept A is true, another concept B is also true, then concept B is a semantic consequence of concept A.' Syntactic consequence is defined as 'if there is proof from concept A to concept B, then concept B is a syntactic consequence of concept A.' Students can progress through their studies by filling out the flashcards with the definitions, notations, and knowledge of the differences between each concept.
・Periodicization
A timeline like the geological era breaks down information hierarchically and is said to be useful for learning long sequences. The geological era is divided into four periods: the Hadean , Archean , Proterozoic , and Phanerozoic . It is important to create flashcards that structure the definitions and durations of each period in stages.
・Rational numbers
The set of rational numbers is defined as the set of fractions with integer numerators and denominators and a non-zero denominator. The flashcards include questions and answers about rational number notation, formal and informal definitions, and set names, and encourage students to create a concept map to help them remember this information.
・Regular expression
We are creating flashcards containing problems for learning regular expressions, progressing from concepts to regular expressions and back again. For regular expression examples, we are creating flashcards for learning concepts such as 'matching the beginning and end of a line' and 'matching numbers using regular expressions.'
·Voltage
Creating flash cards that ask for definitions of voltage in terms of potential and work, and then ask for the terms that correspond to each definition, is said to improve students' understanding of voltage.
Isomers
For 'isomers,' substances that have the same number and type of atoms but different structures, it is important to create flash cards that define terms such as ' structural isomers ,' ' stereoisomers ,' and ' diastereomers ,' as well as flash cards that ask questions about terms from the reverse definition. Creating cards that ask questions from higher-level concepts to lower-level concepts also helps students understand the knowledge.
・Memorizing the months
If you want to memorize months such as 'January is January,' 'February is February,' and 'March is March,' you should create questions such as 'What is the first month of the year?', 'What is the month after January?', and 'What is the month before February?'

・Powers of 2
If you want to memorize things like 2 squared and 2 cubed, it is important to create questions that ask about logarithms in addition to questions like '2 squared is 4' and '2 cubed is 8.'
- Memorizing poems
When you want to memorize a piece of writing, such as a poem, it's important to memorize it in small chunks rather than all at once.
◆Script
Creating flashcards by hand is difficult when applying these learning examples, so Boretti has published a script on GitHub to create flashcards.
◆Software
Many people use Anki , but Boretti says he uses Mochi, which is said to have a better UI than Anki.
Boretti strongly recommends 'understanding before memorizing,' 'keeping flash cards brief,' 'avoiding long sequences,' 'memorizing in order,' 'using simple language,' and 'repeating frequently.'