The secret story of the discovery of the mysterious figure 'hexagon' that appears when folded back even though it is a flat surface.

A figure that can be folded on one side and expanded on another side is called a '
Hexaflexagons-YouTube
Hexaflexagons 2-YouTube
Arthur Harold Stone, who moved from the United Kingdom to the United States in 1939, tried to use American paper sandwiched between British binders and noticed that the paper squeezed out of the binder.

Cut the part that sticks out of the binder with scissors ...

It seems that he was playing with this bundle of paper folded to kill time. Fold, twist, square or hexagon.

After trying various folding methods, a beautiful hexagon was completed.

You might think that a hexagon isn't a big deal, but there's something symmetrical hidden in it. Stone was playing with the completed hexagon folded along the creases ...

If you try to open the mountain part of the crease ...

Notice that the hexagon appears again. It seems that this hexagon can be folded many times like this.

The stone folds the hexagon again.

One side of this hexagon is painted yellow, and the surface is yellow ...

The back side is now white.

If you fold this hexagon again ...

A white surface appears.

Moreover, the back side was also white for some reason.


Paint this white surface green ...

When I turn it back again, a white surface appears again. In other words, you can see that the hexagon of this plane has three faces.

Since we have to give a name to this mysterious figure, Stone names 'Hexagon' by combining 'Bending (Flex)' and 'Hexagon (Hexagon)'.

Furthermore, from the twisted paper ...

Created a flexagon. This completes a more durable flexagon.

Then apply this to orange, yellow and pink.



When this is folded back and round again, a white surface appears again.

Paint this in green and fold it back again.

Then a white surface appears. Paint this in blue.

When I turned it back, I found a whiter surface. It is clear that a total of 6 faces are hidden in a flat hexagon. Therefore, the hexaflexagon with more surfaces is named 'Tri-hexagon'.

The flexagon is easy to make, fold the triangles into bellows and cut the paper to a length that includes nine triangles. Fold it into a hexagon to complete the hexaflexagon. Hexaflexagon is characterized by the fact that the part where the paper is connected forms a rhombus as shown below. To fold it back, just pinch the crevice in the paper inside the hexagon and open it outward.

To unravel the mystery of this mysterious figure, the flexagon, Stone forms a flexagon committee with his friend

To make the tri-hexagon flexagon that attracted the interest of three people, first fold the paper into a bellows to make 18 triangles.

Just fold this into the 'paper with nine triangles' needed to make a hexaflexagon, and then fold it into a hexagon just like you would make a normal flexagon.

After actually folding the tri-hexagon, assign numbers 1 to 6 on each side.

After that, cut the tri-hexagon flexagon once with scissors.

Then, the numbers indicating which side was constructed on the paper are slurried.

Based on this number, paint the surface on which each number is written ...

Make a tri-hexagon again.

When this tri-hexagon is folded back, it circulates on three sides in the order of 1 → 2 → 3 → 1 …….



This is represented by a diagram.
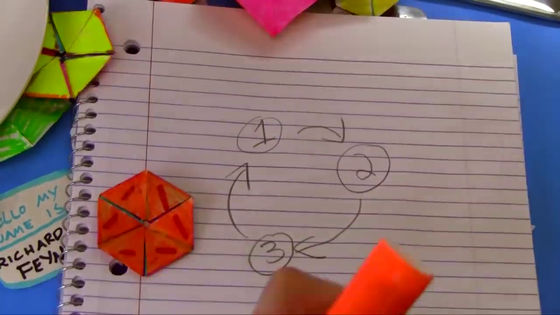
In addition, it is also possible to fold back to 1 → 6, 2 → 5, 3 → 4.
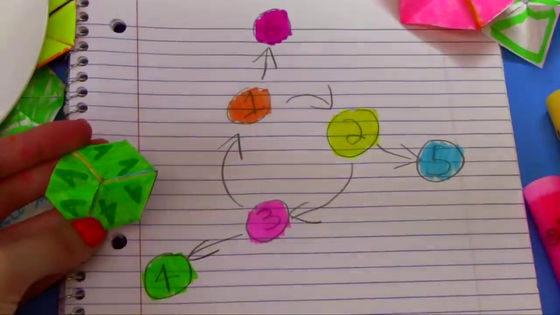
The folding direction from 1 to 6 is one direction, but it can be folded from 6 to 3. However, Tuckerman notices that if you fold in this order, you will not be able to fold 3 → 4. And it is clear that this 3 returns to 6 when folded in the opposite direction, but does not return to 2. In other words, the 3rd surface when folded back in the order of 1 → 6 → 3 is the 3rd surface that looks the same but is different from the usual one.
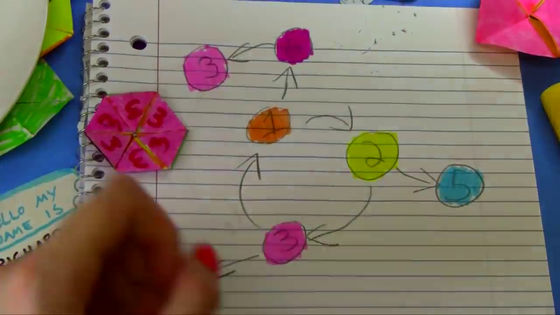
So, let's draw a star in the center of 3.

And when you fold it in the order of 1 → 6 → 3 ……


The star pattern moves from the inside to the outside of the hexagon.

By investigating how the other aspects are related in the same way, the following diagram is completed.
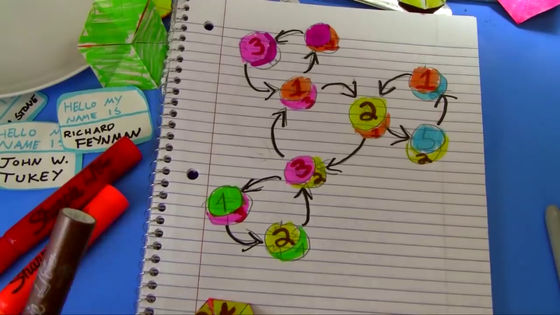
Eventually, this diagram will be called the 'Feynman diagram' after a friend who advised him to draw a star pattern.

Then, in 1941, the United States entered World War II, and Stone et al.'S quest for hexaflexagon came to an end. However, in 1956, mathematician and amateur illusionist

I asked a friend to show me a cloth hexaflexagon and learned about the existence of a hexaflexagon.

Gardner is also famous for serializing a column called 'Mathematical Games' in the academic journal Scientific American from 1956 to 1981. Hexaflexagon is said to have become known throughout the United States as Gardner introduced it in this column.

Related Posts:
in Video, Posted by logu_ii







