A movie that creates 'a basketball goal that you can definitely score if you shoot'

How I made a basketball hoop that always goes in-YouTube
The basketball goal created by Stuff Made Here is 'a basketball goal where the ball enters the goal no matter where it hits the backboard'. The prototype was the SKLZ basketball practice goal pro mini hoop 004015, which is a basketball for home use sold at Amazon and others, and Stuff Made Here makes his own backboard.

Wherever the ball hits the basketball backboard ...


The ball passes the ring and reaches the goal.

Looking at 'Basket goal where the ball enters the goal no matter where it hits the backboard', it looks like this when the angle is changed. Except for the goal ring, it is completely self-made, and the point is that it has a curved surface unlike a normal backboard.

To create a 'basket goal where the ball hits the goal no matter where you hit the backboard', you need to calculate the shape of the backboard. For that, various programming will be necessary.

Stuff Made Here uses a
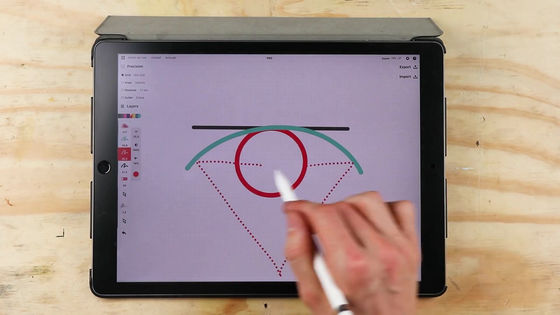
A normal basketball goal has a square frame drawn just to the side of the goal ring, and it is believed that hitting the ball here will enter the goal. The size of the frame of this quadrangle is 45 cm long × 59 cm wide, and the line thickness is set to 5 cm.

In other words, simply speaking, if the ball hits outside this frame, it will not enter the goal. So Stuff Made Here wanted to extend this frame to the entire backboard so that the ball would hit the goal no matter where it hits the backboard.
In order to get into the goal no matter where the ball hits on the backboard, the backboard needs to be reshaped. Considering only the lateral movement, it should be possible to make the ball enter the goal wherever it hits by making the backboard a curved surface as follows.
The same is true for the vertical direction.
It is difficult to understand this shape accurately and reproduce it as a backboard. The
The shape derived at the end of such a simulation is 'a shape like a parabolic antenna for receiving satellite broadcasts,' Stuff Made Here explains. The parabolic antenna has a bowl-like shape, and is a shape for reflecting the radio waves flying in parallel so that one point is concentrated on the axis part of the antenna.

Radio waves can fly straight to the parabolic antenna, but the trajectory of the ball that hits the backboard of the basket goal is parabolic. Therefore, the trajectory of the ball that bounces off the backboard is also parabolic. In addition, the trajectory of the ball bouncing off the backboard also changes depending on the speed of the shot, so it is necessary to calculate the backboard shape taking these into consideration.
In addition, basketball sometimes hits the backboard from the bottom and bounces upward. However, this time I decided to create a backboard to make sure that only those that fly in the orbit of a mountain arch line can enter the goal.
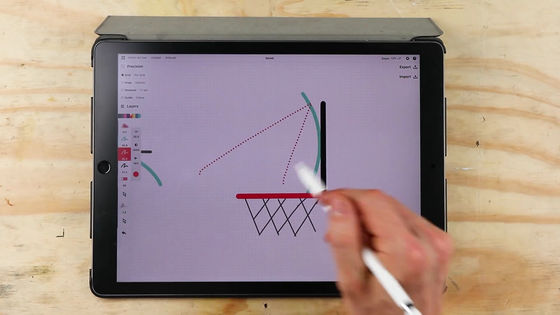
The basketball attached to the 'SKLZ basketball practice goal pro mini hoop 004015' was smaller than the 6.5 size basketball used in NBA etc., so even if the shot strength is different to some extent, it is the same. It seems that there were cases where the ball entered the goal if it was on the trajectory.
Thousands of simulations of shooting from various positions on the basket court using the Monte Carlo method were performed, and thousands of calculations were made to say, 'If you shoot from this angle, the backboard will enter the goal if this angle'. Executed a million times.
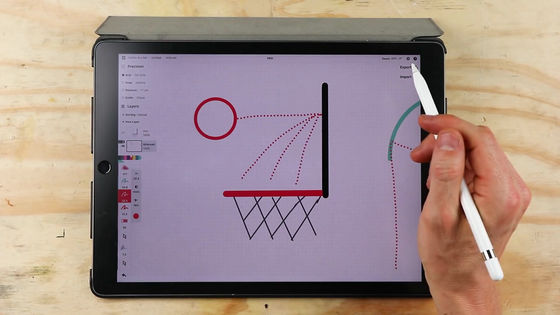
The image below is a simple representation of the basketball court, where the red circle is the goal ring.
Below, the red dotted line represents the trajectory of the ball, and the blue angle represents the 'angle at which the ball enters the goal.'
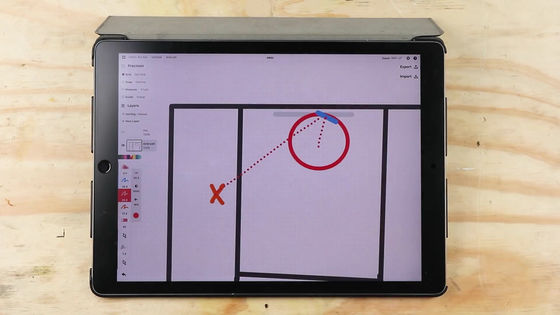
At the same point on the backboard, if the type of shot (speed or angle) is different, the trajectory of the ball after bouncing will also be different, so it is necessary to proceed with the calculation while keeping all balance.
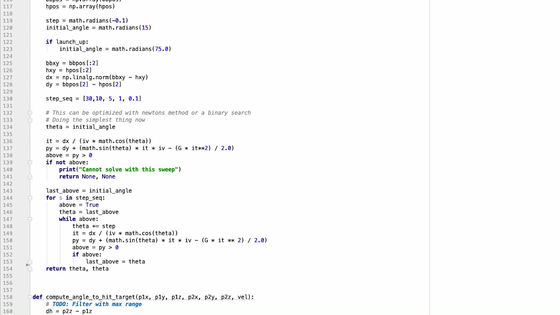
Naturally, the simulation is done on programming, and part of it is released in the movie.
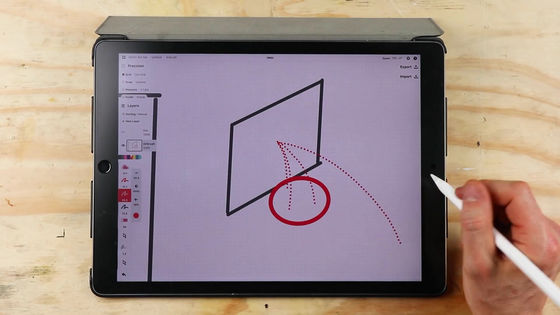
The image below shows a simulation of 16 different trajectory shots from one location.
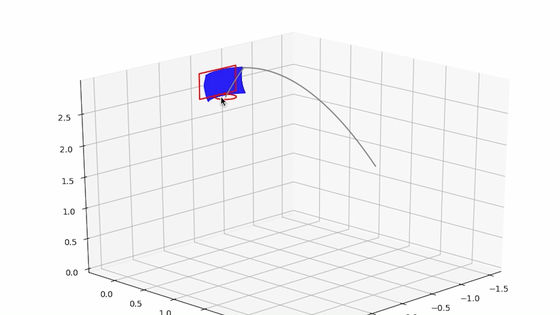
In this way, the optimum angle is derived for all points on the backboard, and the backboard shape is created from these numbers. The shape of the backboard is created with 3D CAD software

Then, the wood is processed using 1100MX, a

The following parts were completed in this way.

When the parts are assembled, it becomes a backboard on the curved surface that appeared at the beginning of the movie.


That's why Stuff Made Here's 'Basket Goal with a Ball' is completed.

When I actually shot it, I never got into the goal and the ball hit the ring many times. It seems that this was a problem that occurred because the thickness of the ring and the radius of the ball were not taken into consideration, but it seems that it was solved by moving the position of the ring slightly forward.

In addition, how to throw the ball is also important, and it is said that it will be possible to definitely score the goal by hitting the ball on the backboard without directly aiming at the goal ring.

Related Posts:
in Video, Posted by logu_ii







