Sep 13, 2020 20:00:00

A movie explaining 'Is an orbital elevator feasible?'

An '

orbital elevator ' is an elevator that has an orbit that extends from the surface of a planet to more than a geosynchronous orbit, and it is thought that if it is realized, it will be possible to go to space at a much lower cost than a rocket. The scientific YouTube channel Real Engineering actually used mathematical formulas to answer the question, 'Is such an orbital elevator really realized?'

Are Space Elevators Possible? --YouTube


An orbital elevator is a huge elevator shaft that connects the surface of the earth with space. If this is achieved, it is said that the cost of going to space will be greatly reduced because it will not be necessary to rely on rockets to go into orbit.

Building an orbital elevator requires a completely different material than normal buildings, which require strong

compressive strength .

In ordinary buildings, the problem of weight is solved by increasing the area of the foundation and making it thinner as it rises. The most extreme example is the pyramid.

The same is true for

Burj Khalifa , the tallest skyscraper in the world.

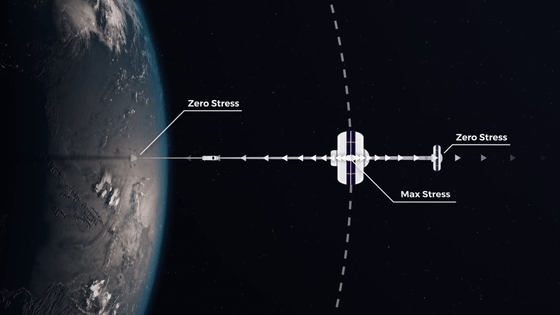
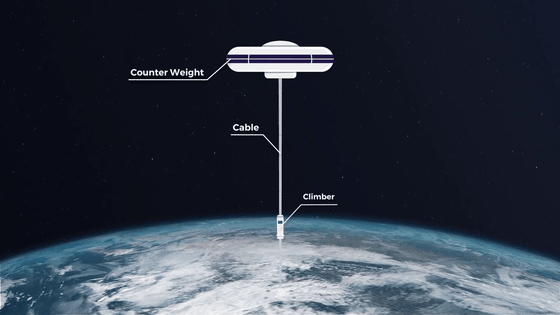
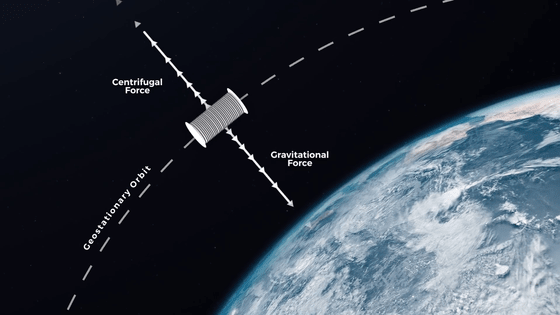
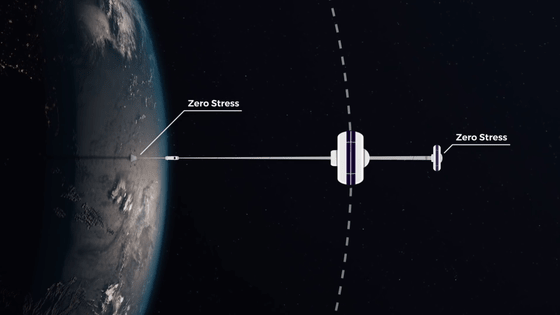
Orbital elevators, on the other hand, are equipped with end parts with huge mass called 'counterweights'. The counterweight is subjected to outward centrifugal force due to the rotation of the earth, and the tether, which is the pillar of the orbital elevator, is pulled toward the universe, so it is 'the most on the lowest level' like a building on the earth. There is no such thing as 'weighting'.

In order for the orbital elevator to stay in a stable circular orbit, it is necessary to find a point where the centrifugal force and gravity are balanced, so first calculate the height at which the centrifugal force and gravity are balanced.

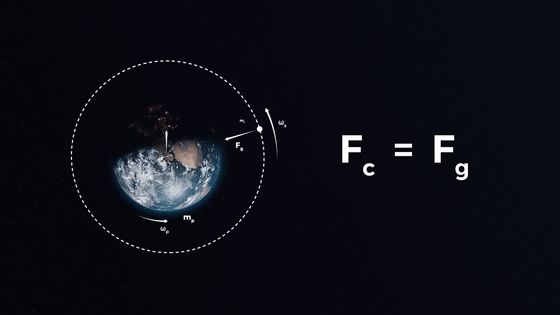
Below is a diagram for calculating centrifugal force and gravity. 'M _s ' is the mass of the satellite, 'ω (omega)' is the

angular velocity , 'r' is the distance to the center of the earth, 'G' is the gravitational constant , and 'm _p ' is the mass of the earth.

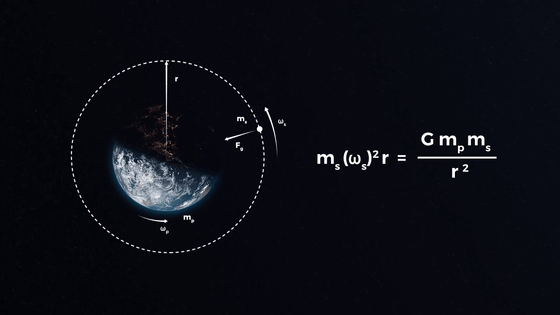
Turn off the 'm _s' on the both sides, such a feeling in the form of 'r ='.

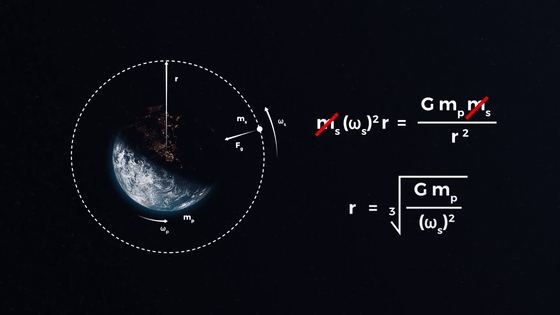
The answer to this question is 'about 36,000 km', which is obtained by substituting the value into this formula and subtracting the radius of the earth from '42,168 km'.

Since it is impossible to construct a structure with a height of about 36,000 km from the ground, an orbital elevator construction method has been devised to extend the tether from a huge satellite to the surface of the earth.

However, if you extend the tether toward the surface of the earth, the center of gravity will shift and the satellite will fall. Therefore, it is necessary to extend the tether while maintaining the position of the center of gravity by installing a counterweight on the opposite side of the tether.

Gravity increases and centrifugal force weakens as you approach the earth, so the tether stretched to the surface of the earth exerts a strong force toward the surface of the earth. On the other hand, as you get closer to the universe, gravity weakens and centrifugal force increases, so the tether extended toward the universe exerts a strong force toward the universe. As a result, the center point of the tether extending to the surface of the earth and the tether extending to the universe will be pulled with a very strong force.

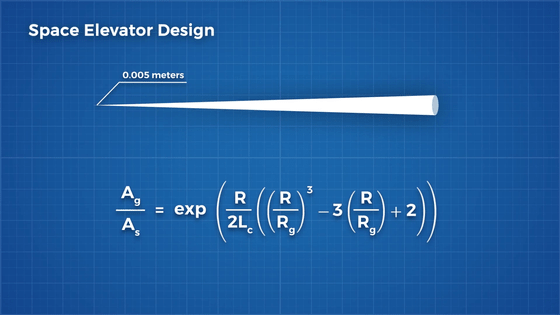
The force received by the tether can be calculated by the following formula. 'G' is the gravitational constant, 'M' is the mass of the earth, 'ρ (low)' is the density of the tether material, 'R' is the radius of the earth, and 'R _g ' is the radius of the

geosynchronous orbit .

Let's calculate what kind of material can withstand this force. As a test, assuming that the tether is made entirely of steel, substitute the density of steel, 7900 kilograms per cubic meter, into 'ρ' ...

The maximum

tensile stress is 382 Giga Pascal . This is 240 times the strength of steel.

However, the lower the density than steel, the less tensile stress is required. In addition, the tether can be made thinner because it exerts almost no force near the surface of the earth or near the counterweight.

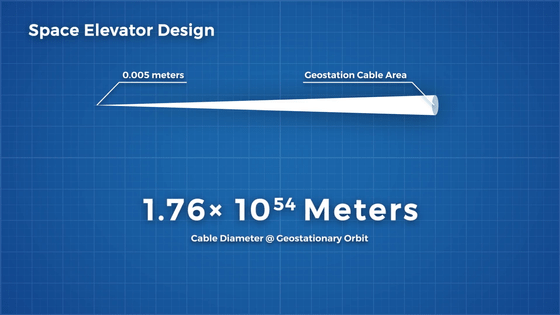
Therefore, let's assume that the thinnest part is 5 mm.

Next, let's calculate the diameter of the thickest part. If steel is used, the diameter of the thickest part is 1.76 x 10 to the 54th meter. Since the known size of the universe is 8.8 x 10 26 meters, the result is that theoretically much thicker steel is needed than the universe. This means that it is impossible to build orbital elevators with steel.

It is calculated that the thickness of

carbon fiber composite material is 170 meters and that of Kevlar fiber is 80 meters, but it is not realistic to make Kevlar fiber with a thickness of 80 meters.

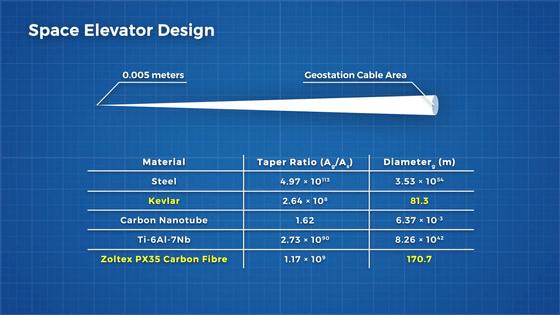
If you try to make it, the cost will outweigh the benefits of orbital elevators.

So, the answer to the question 'Is an orbital elevator feasible?' Is 'There is no material to make.'

But it may not be impossible forever. One of the promising materials for orbital elevators is

carbon nanotubes .

The strength of carbon nanotubes is astounding, with one study showing that the maximum tensile stress is as high as 130 gigapascals and the density is only 1300 kilograms per cubic meter.

However, there are many engineering challenges for the practical application of carbon nanotubes.

In a future series, Real Engineering will explore other issues with orbital elevators, such as what challenges carbon nanotube manufacturing has and how to deal with tether vibrations and climate.