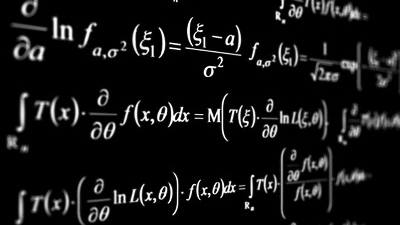There is a mathematician who is challenging with 'Gachinko' in 'How many seconds will it mix perfectly if you stir the cards on the desk?'

by
Prof. Persi Diakonis , a statistic teacher at Stanford University, is a unique mathematician who has worked as a professional magician and has made many achievements in research on randomness such as coin toss and card shuffle. What Mr. Diakonis is challenging as “the biggest mystery of shuffle” is the problem of “smoothing”, a primitive shuffle method that stirs cards on the desk.
Persi Diaconis Mixes Math and Magic | Quanta Magazine
https://www.quantamagazine.org/persi-diaconis-mixes-math-and-magic-20150414/
◆ What is smoothing?
When you play the following movie, you can see the former professional magician Diaconis demonstrating the card shuffle.
The Best (and Worst) Ways to Shuffle Cards-Numberphile-YouTube
Diaconis has already found in various studies how many shuffles can be used to determine how many times the deck can be shuffled to make it completely random. For example, in a ruffle shuffle that mixes the cards divided into two like this, it is OK if you do it 7 times.

On the other hand, familiar

The shuffling method of mixing cards on the desk is called “smoothing” and is sometimes called

◆ Smoothing research
It's easy to do smoothing, but it's hard to solve the card movements mathematically, and the question 'How long can it be random?' Has not yet been answered. According to Diakonis, 'The movement of the card when smoothing is close to a hydrodynamic phenomenon.' One example of this phenomenon is the movement of marine litter carried by ocean currents.
Fluid dynamics is a field that is very difficult to fully elucidate.For example, the mystery of solving the Navier-Stokes equation, one of the important pillars of fluid dynamics, is counted as one of the unsolved problems in physics . .
Diaconis is tackling this problem by researching the Markov chain Monte Carlo method, a computational technique widely used in the field of statistics. Diakonis believes that integrating fluid mechanics and statistics is the way to approach the mystery of smoothing.
Another clue to Diaconis's research is the “cut-off phenomenon”. It seems that if you shuffle the cards, the deck will seem to be random as much, but in the past research of Mr. Diakonis, `` the deck being shuffled is suddenly random at a certain timing '' I know. This “rapid random” phenomenon is the cut-off phenomenon.
It is known that all shuffle methods such as ruffle shuffle that Diakonis has solved so far have caused the cut-off phenomenon, so if you know that the cut-off phenomenon will occur even with smoothing, it will be perfect in seconds. It becomes a serious clue to find out if it is random.
◆ Experiment
Diakonis, a practicing statistician, has already been experimenting with smoothing. Diaconis worked with Stanford University biostatisticians Marc Kolam and Lauren Bandklayder and the students to smooth each of 15 seconds, 30 seconds, and 1 minute each time, and did the deck actually become random? I examined it.
The best way to find out if a deck is random is to look at the percentage of decks in the same order, but this is not practical. Because there are 52 kinds of cards in the way of the 52 cards, the calculation result of the factorial of 52 is closer to the estimated number of atoms in the galaxy. Because it becomes a big number. As a result, it is said that `` the possibility that the arrangement of well-cut cards has become the same since history is almost zero '', and it is almost the same arrangement with 100 or 200 shuffles There is none.

by Nejron
So Diakonis tested the results of the smoothing shuffle using 10 different statistical methods. For example, tests such as “Where a specific card has moved to a deck” or “Check the number of times a continuous card has been consecutive after shuffling, like spades 1 and 2.”
As a result, 15 seconds of smoothing failed to pass the test as Diakonis expected. On the other hand, betraying Mr. Diaconis's expectation that “It would be difficult to pass all tests even with 1 minute smoothing”, smoothing for 30 seconds and 1 minute passed all 10 tests. From this result, Diakonis sees that “the smoothing length that can make the deck perfectly random is within one minute”. However, in fact, the sample count of 100 is not statistically reliable.
It is said that Mr. Diakonis needs at least 10,000 times to make a convincing conclusion, but it would be distracting to shuffle 10,000 times each in 15 seconds to 1 minute And it is impossible at all by Mr. Diakonis and colleagues. Therefore, Mr. Diakonis said that he plans to proceed with the “National Smoothing Plan” that will allow him to do smoothing in mathematics classes at junior high schools and high schools in the United States.
It is unclear how serious Mr. Diakonis's `` National Smoothing Plan '' is, but since Mr. Diakonis ran away at the age of 14 and jumped into the magician world, he spent more than 50 years researching shuffles Considering that, the shuffle passion is definitely real.
Related Posts: