What is the ratio of "technology" and "luck" in sports? And why do people enjoy sports

ByChris Brooks

Many of the people who like sports such as baseball and soccer are thrilled and worried about the results of the team that they support and are watching the way of the season. Scientific analysis has been introduced to the world of professional sports for a long time, but it is still one of the real pleasures to watch sports that even unexpected results will arise. In the world of such sports, movies that explain the proportion occupied by "competition" of players and "luck" at that time depends on the competition and ultimately "question why we enjoy sports" is released It is being done.

Why underdogs do better in hockey than basketball - YouTube


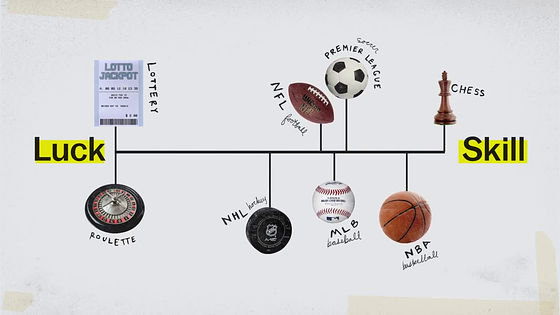
Analyzing the proportion of "luck" and "technology" in professional sports based on a certain theory, it is like this when arranging in line. The thing that depends on "luck" the leftmost is represented by gambling, and the one on the far right is "technology" like chess, NHL (ice hockey) is the most lucky, then NFL (American football), MLB (Major League), followed by football's Premier League, NBA (basketball) has the result that results are influenced most by player's skill.


This is Mr. Michael Mobsin, who carried out this analysis.


Mr. Mobinsen wrote the book "The Success Equation" from which you can see why we like various sports.


According to Mr. Mobinsen, the NBA is the sport most distant from "luck". Conversely, hockey is the most sports with "randomness".


Mr. Mobinsen says, "All the athletes have a fantastic skill, they are tremendously wonderful technicians."


The biggest meaning in mathematical expressions is "sample size", that is, the number of games in one season. Baseball's major league fights 162 games a year, but only 16 games in NFL.


Due to the small sample size, NFL has more elements of luck than technology.


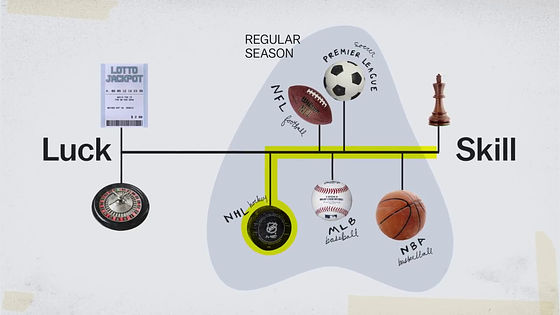
But that is not the only factor that determines everything. Both NHL and NBA fight 82 games per season, but the position of the graph is different. The important factor here is "game dynamism".


This is "How many turns must I score per game?" This is also counted as one element of the sample size. In the case of basketball, the number of shots increases as the time from holding the ball to shooting is fixed.


In the case of ice hockey, the game is more fluid and more difficult to measure which team owns the pack in the first place.


The number of players will also affect the evaluation. In the case of tennis fighting with one or two people, the way the game is played depends largely on the skill of the player himself.


As a result, it is possible that a competent player like Serena Williams monopolizes the top ranking ranking from 2013 to 1816 in 2016. In other words, in the case of sports where technology is a major factor in the outcome of the game, it is relatively easy to predict the outcome.


However, in sports such as basketball, football and baseball where multiple players fight with teams, many factors will be involved in the outcome of the game.


In the case of baseball fighting by nine people, eight players need to stand at the battle before the next batting order comes.


According to Mr. Mobinsen, "Ideally it is the case that the batting order that all batters hit is configured, but that is impossible."


"But in the case of basketball there is something close to that, it is often the case that star players like Lebron / James play a big success in both defense and lead the team to triumph."


"In addition, even at ice hockey, players like Sydney Crosby will be out of the game and decide where to go," Mr. Mobinsen said. In the case of ice hockey with a fast flow of games and a large amount of exercise, even top players need to take turns while taking a break and take a break, but in rare cases top players continue to play and play the game advantageously That is why.


Even in the case of football, "quarterback" playing the role of the team's command tower is the key to attack.


Mr. Mobinsen says "Football is the sport that is consolidated into several excellent players, where the combination of quarterback and coach will be the most important factor in winning the game."


And what becomes important here is "talent pool", that is, how thick the excellent players' layers are.


In basketball, as the table below shows, there are many players who are very tall compared to baseball, ice hockey and American football.


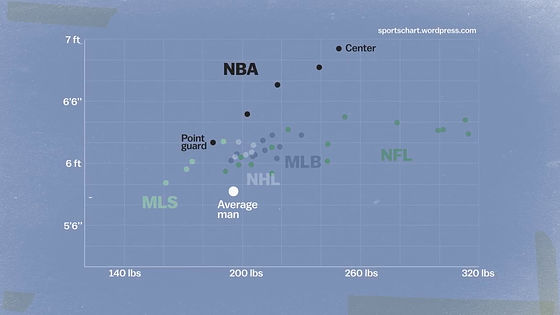
"If you reduce the sample size, there is a stochasticDispersion. Even basketball players with a height of 2 meters, there are players with skills and players who are not. However, there are players who are playing at NBA because "Height is high". As a result, the dispersion becomes more, so the presence or absence of technology will make a big meaning. "


Meanwhile, soccer and ice hockey do not require unusual physique like basketball. For this reason, the way the game goes depends more on being influenced by "luck".


The mathematical expression "Pythagorean Theorem of Statistics of statistical theory" that Mr. Mobinsen used was taught from a sports analysis expert to indicate this.


This formula shows that these variables can be added when there are two random and independent variables. When applying this case, it is a factor that determines what adds technology and luck appears as a solution as an actual result, that is, the content of what technology and luck will actually happen.


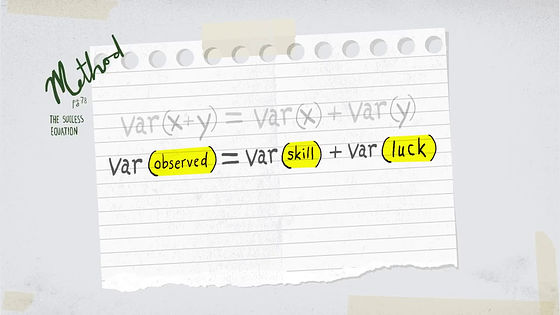
As the number of games per season decreases, the luck is reduced.


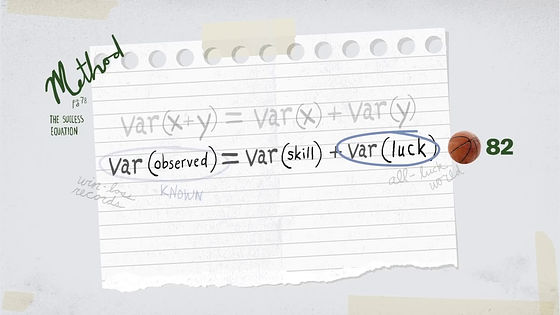
This is the same as increasing the number of times you do coin tos, the proportion of the front and back comes closer to 50:50.


Depending on the mechanism of the equation, subtracting luck factors from actual results leads to the amount of required technology.


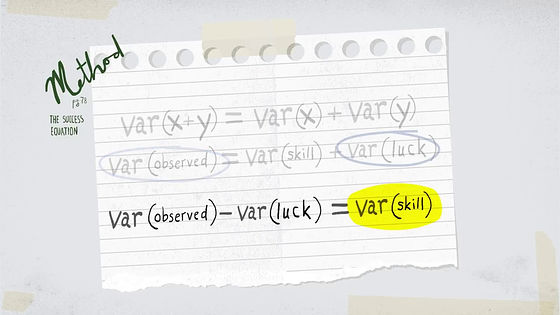
And figures derived from NBA, Football's Premier League, Major League Baseball, NFL, NHL are elements of luck. There are statistics that NBA has the lowest element of luck and NHL is the most lucky.


On the other hand, if you look at the playoff situation at the end of the season, you will see different results. According to a statistic, baseball is "the strongest team will win" is the most uncertain sport.


From here, the question comes to us, "What do we want for sports?"


"Our fans are cheering for teams to enjoy good and bad times together"


"I think that's what we have for human beings, and I feel that it is fun to see the game because of that," Mobbsin says.